Cilindro
O cilindro circular é o sólido obtido ao transladar um círculo ao longo de uma reta paralela ao seu eixo. Quando a reta é perpendicular às bases, temos o cilindro reto; quando é inclinada, o cilindro oblíquo. O cilindro é um dos corpos redondos fundamentais, ao lado da esfera e do cone.
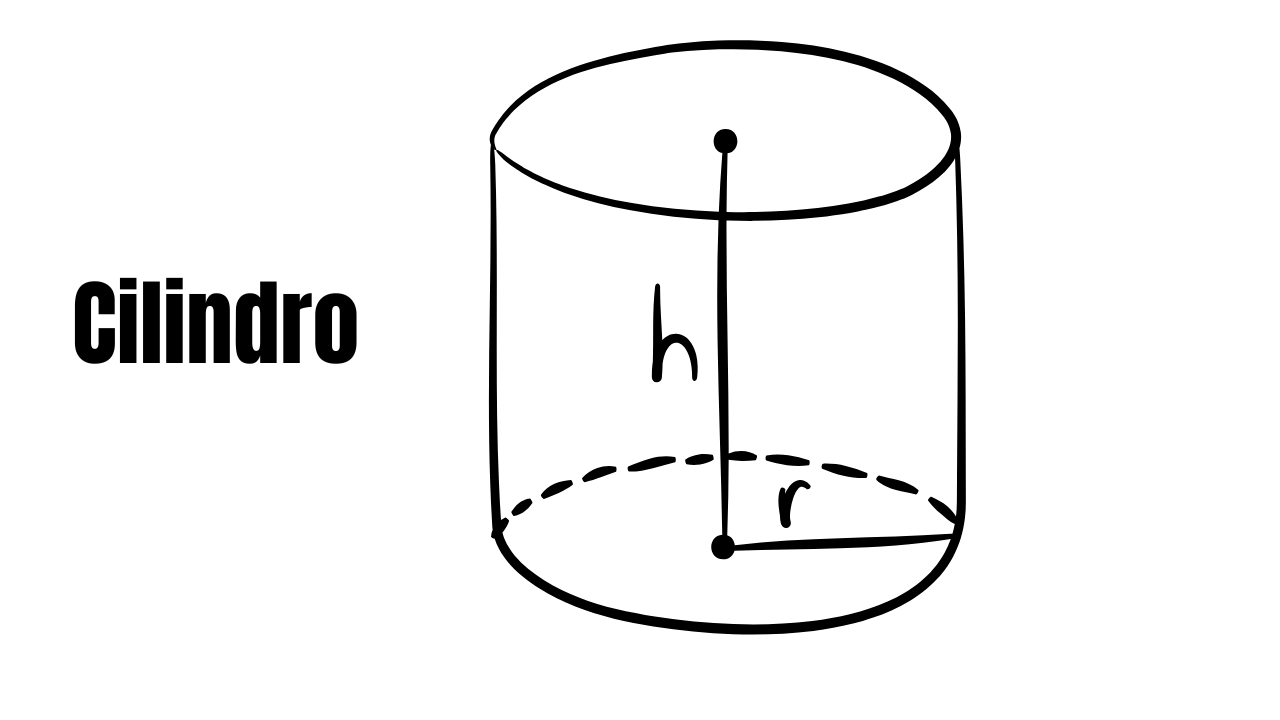
Notação que usaremos no artigo: \(r\) = raio da base (raio do círculo da base), \(h\) = altura (distância perpendicular entre os planos das bases), \(g\) = geratriz (tamanho da lateral inclinada no oblíquo), \(A_L\) = área lateral, \(A_T\) = área total e \(V\) = volume.
Elementos e tipos
- Bases: dois círculos congruentes de raio \(r\).
- Altura \(h\): distância perpendicular entre os planos das bases.
- Geratrizes: segmentos paralelos à altura que “formam” a superfície lateral; no reto, a geratriz coincide com \(h\); no oblíquo, a geratriz tem comprimento \(g\) e é inclinada.
- Cilindro reto: eixo perpendicular às bases; a planificação lateral é um retângulo \(2\pi r \times h\).
- Cilindro oblíquo: eixo inclinado; a planificação lateral é um paralelogramo \(2\pi r \times g\).
Fórmulas essenciais
Área lateral (reto): \(\displaystyle A_L=2\pi r h\).
Área lateral (oblíquo): \(\displaystyle A_L=2\pi r g\) (perímetro da base × geratriz).
Área total (reto): \(\displaystyle A_T=A_L+2\pi r^2=2\pi r(h+r)\).
Volume (reto/oblíquo): \(\displaystyle V=\text{área da base}\times \text{altura}=\pi r^2 h\).
Escalonamento: se \(r\to k r\) e \(h\to k h\), então \(A\to k^2A\) e \(V\to k^3V\).
Relações úteis: com mesma base e altura, \(V_{\text{cil}}=3\,V_{\text{cone}}\). Para uma esfera inscrita em cilindro com raio \(r\) e altura \(2r\), \(V_{\text{esf}}/V_{\text{cil}}=2/3\) e \(A_{\text{esf}}=A_L\) do cilindro.
Planificação
A superfície lateral do cilindro reto “abre” num retângulo de dimensões largura \(=2\pi r\) (circunferência da base) e altura \(=h\). Esse retângulo é exatamente a área do rótulo de uma lata.
| Peça | Dimensões | Área |
|---|---|---|
| Lateral (reto) | \(2\pi r \times h\) | \(2\pi r h\) |
| Cada tampa | círculo de raio \(r\) | \(\pi r^2\) |
| Total | — | \(2\pi r h+2\pi r^2\) |
Exemplos resolvidos
Capacidade de uma lata
Uma lata cilíndrica tem raio interno \(r=3{,}5\) cm e altura \(h=12\) cm. Qual a capacidade em litros?
Ver solução
\(V=\pi r^2 h=\pi\cdot3{,}5^2\cdot12=147\pi\approx 461{,}8\ \text{cm}^3= \mathbf{0{,}462\ L}\).
Área do rótulo
Para uma lata com \(r=3\) cm e \(h=10\) cm, determine a área do rótulo (apenas a área lateral).
Ver solução
\(A_L=2\pi r h=2\pi\cdot3\cdot10=60\pi\approx \mathbf{188{,}5\ \text{cm}^2}\).
Menor área total para volume fixo
Entre cilindros de volume \(V\) fixo, o de menor área total ocorre quando \(h=2r\). Com \(V=1000\ \text{cm}^3\), calcule \(r\) e \(h\).
Ver solução
\(h=2r\Rightarrow V=2\pi r^3\Rightarrow r=(V/2\pi)^{1/3}\approx \mathbf{5{,}42\ \text{cm}}\) e \(h\approx \mathbf{10{,}84\ \text{cm}}\).
Exercícios (enunciados claros + soluções em abre/fecha)
Definições usadas nos enunciados: \(r\) = raio da base (raio do círculo da base); \(h\) = altura do cilindro (distância perpendicular entre os planos das bases); \(g\) = geratriz do cilindro oblíquo (comprimento da lateral inclinada).
1) Uma lata cilíndrica tem raio da base \(r=3{,}5\) cm e altura \(h=12\) cm. Qual é a capacidade em litros?
- 0,40 L
- 0,46 L
- 0,50 L
- 0,60 L
Solução
\(V=\pi r^2h=147\pi\approx 0{,}4618\) L → 0,46 L.
2) Uma lata possui raio da base \(r=3\) cm e altura \(h=10\) cm. Qual é a área do rótulo (apenas a superfície lateral da planificação)?
- 150 cm²
- 175 cm²
- 188,5 cm²
- 210 cm²
Solução
\(A_L=2\pi r h=60\pi\approx \mathbf{188{,}5\ \text{cm}^2}\).
3) Um cilindro oblíquo tem raio da base \(r=5\) cm e geratriz \(g=13\) cm (comprimento da lateral inclinada). Calcule a área lateral.
- \(60\pi\ \text{cm}^2\)
- \(100\pi\ \text{cm}^2\)
- \(120\pi\ \text{cm}^2\)
- \(130\pi\ \text{cm}^2\)
Solução
\(A_L=2\pi r g=2\pi\cdot5\cdot13=\mathbf{130\pi\ \text{cm}^2}\).
4) Um vaso cilíndrico reto tem raio da base \(r=4\) cm e altura \(h=15\) cm. Determine a área total (lateral + duas tampas).
- \(120\pi\ \text{cm}^2\)
- \(144\pi\ \text{cm}^2\)
- \(152\pi\ \text{cm}^2\)
- \(168\pi\ \text{cm}^2\)
Solução
\(A_T=2\pi r(h+r)=2\pi\cdot4(15+4)=\mathbf{152\pi\ \text{cm}^2}\) (≈ 477,5).
5) Um cilindro tem raio da base \(r\) e altura \(h=2r\). Ele contém uma esfera inscrita. Que fração do volume do cilindro é ocupada pela esfera?
- 1/2
- 2/3
- 3/4
- 4/5
Solução
\(V_{\text{esf}}/V_{\text{cil}}=\dfrac{4/3\,\pi r^3}{2\pi r^3}=\mathbf{2/3}\).
6) Uma lata tem raio da base \(r=4\) cm e altura \(h=12\) cm. Na planificação, o rótulo é um retângulo cuja largura é \(2\pi r\) e a altura é \(h\). Quais as dimensões desse retângulo?
- \(8\pi\) cm × 12 cm
- \(12\pi\) cm × 8 cm
- 16 cm × \(4\pi\) cm
- 25 cm × 12 cm
Solução
Largura \(=2\pi r=8\pi\approx 25{,}13\) cm; altura \(=12\) cm → alternativa A.
7) Dois cilindros têm o mesmo volume. A: \(r=4\) cm (raio), \(h=10\) cm (altura). B: \(r=5\) cm, \(h=6{,}4\) cm. Qual usa menos área lateral (menor rótulo)?
- A
- B
- Iguais
- Indecidível
Solução
Áreas laterais: A \(=2\pi\cdot4\cdot10=80\pi\); B \(=2\pi\cdot5\cdot6{,}4=64\pi\). Menor: B.
8) Para volume fixo \(V=1000\ \text{cm}^3\), o cilindro de menor área total atende \(h=2r\). Quais valores aproximam melhor \(r\) (raio da base) e \(h\) (altura)?
- \(r=4{,}8\) cm; \(h=9{,}6\) cm
- \(r=5{,}4\) cm; \(h=10{,}8\) cm
- \(r=6{,}0\) cm; \(h=12{,}0\) cm
- \(r=7{,}0\) cm; \(h=14{,}0\) cm
Solução
\(r=(V/2\pi)^{1/3}\approx 5{,}42\) cm; \(h\approx 10{,}84\) cm → mais próxima: B.
9) Um tarugo cilíndrico de alumínio tem raio da base \(r=4\) cm e altura \(h=20\) cm. A densidade do alumínio é \(2{,}7\ \text{g/cm}^3\). Qual é a massa do tarugo?
- 1,80 kg
- 2,10 kg
- 2,71 kg
- 3,00 kg
Solução
\(V=\pi r^2h=320\pi\approx 1005{,}31\ \text{cm}^3\). Massa \(=2{,}7\cdot V\approx \mathbf{2{,}71\ \text{kg}}\).
10) Num cilindro reto, a área lateral é \(A_L=250\pi\ \text{cm}^2\) e o raio da base é \(r=5\) cm. Determine a área total (lateral + duas tampas). Lembre: a altura \(h\) é a distância entre as bases.
- \(300\pi\ \text{cm}^2\)
- \(350\pi\ \text{cm}^2\)
- \(400\pi\ \text{cm}^2\)
- \(450\pi\ \text{cm}^2\)
Solução
De \(A_L=2\pi r h\Rightarrow h=\dfrac{250\pi}{2\pi\cdot5}=25\) cm. \(A_T=2\pi r(h+r)=2\pi\cdot5(25+5)=\mathbf{300\pi\ \text{cm}^2}\).






















