Circunferência: Raio, Diâmetro e Cordas

Revisamos as principais definições e propriedades da circunferência: raio, diâmetro, cordas, arco, tangente e secante. Trazemos ainda fórmulas úteis, exemplos resolvidos e exercícios para praticar.

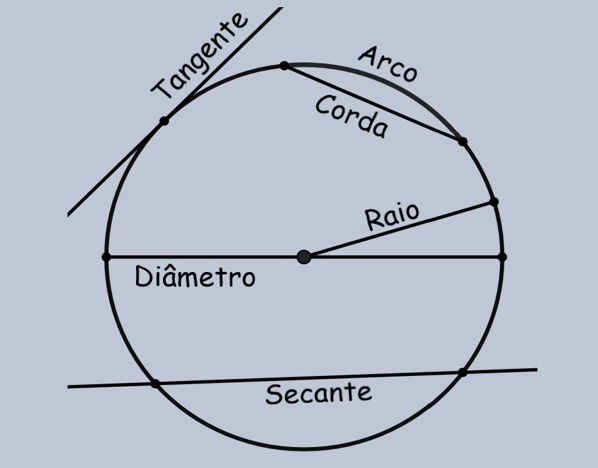
Circunferência com raio, diâmetro, corda, arco, tangente e secante — Elementos da circunferência: raio, diâmetro, corda, arco, tangente (raio ⟂ tangente no ponto de contato) e secante.

Conteúdos relacionados: Comprimento da Circunferência, Área do Círculo, Área do Setor Circular, Lei dos Senos e Lei dos Cossenos.

Definições rápidas

Raio (r): segmento do centro a qualquer ponto da circunferência.
Diâmetro (d): corda que passa pelo centro. Vale \(d=2r\).
Corda: segmento que une dois pontos da circunferência (nem sempre passa pelo centro).
Arco: parte da circunferência entre dois pontos.
Tangente: reta que toca a circunferência em um único ponto e é perpendicular ao raio nesse ponto.
Secante: reta que intercepta a circunferência em dois pontos.

Fórmulas úteis (empilhadas)

\[ \textbf{1) Relação básica:}\quad \boxed{d=2r} \]

\[ \textbf{2) Comprimento da circunferência:}\quad \boxed{C=2\pi r=\pi d} \]

\[ \textbf{3) Comprimento do arco:}\quad \boxed{L=\frac{\alpha}{360^\circ}\,2\pi r = r\theta}\quad (\theta \text{ em rad}) \]

\[ \textbf{4) Tamanho da corda pelo ângulo central }(\alpha):\quad \boxed{c=2r\sin\!\left(\frac{\alpha}{2}\right)} \]

\[ \textbf{5) Tamanho da corda pela distância ao centro }(x):\quad \boxed{c=2\sqrt{\,r^2-x^2\,}} \]

\[ \textbf{6) Propriedade da tangente:}\quad \text{o raio ao ponto de tangência é perpendicular à tangente} \ (r\perp t) \]

\[ \textbf{7) Tangentes a partir de um mesmo ponto externo }(P):\quad \boxed{PA=PB}\ (\text{comprimentos iguais}) \quad\text{e}\quad \boxed{PT^2=PO^2-r^2} \]

Exemplos resolvidos (situação-problema)

Corda por ângulo central

Um disco tem raio \(r=10\,\text{cm}\). Dois pontos definem um ângulo central de \(\alpha=60^\circ\).

Dados: \(r=10\,\text{cm}\), \(\alpha=60^\circ\).

Qual é o comprimento da corda que une esses pontos?

Ver solução

\[ \begin{aligned} c&=2r\sin\!\left(\frac{\alpha}{2}\right)\\ &=2\cdot 10\cdot \sin 30^\circ\\ &=20\cdot \tfrac12\\ &=\boxed{10\ \text{cm}} \end{aligned} \]

Corda pela distância ao centro

Numa circunferência de raio \(r=8\,\text{cm}\), uma corda está a \(x=3\,\text{cm}\) do centro.

Dados: \(r=8\,\text{cm}\), \(x=3\,\text{cm}\).

Qual é o comprimento dessa corda?

Ver solução

\[ \begin{aligned} c&=2\sqrt{r^2-x^2}\\ &=2\sqrt{8^2-3^2}\\ &=2\sqrt{64-9}\\ &=2\sqrt{55}\\ &\approx \boxed{14{,}83\ \text{cm}} \end{aligned} \]

Diâmetro, raio e arco

Uma pista circular tem diâmetro \(d=14\,\text{m}\). Deseja-se marcar um arco de \(\alpha=45^\circ\).

Dados: \(d=14\,\text{m}\Rightarrow r=7\,\text{m}\); \(\alpha=45^\circ\).

Calcule \(C\) e o comprimento do arco \(L\).

Ver solução

\[ \begin{aligned} C&=\pi d=\pi\cdot 14=14\pi\ \text{m}\\[4pt] L&=\frac{\alpha}{360^\circ}\,2\pi r\\ &=\frac{45^\circ}{360^\circ}\cdot 2\pi\cdot 7\\ &=\frac{1}{8}\cdot 14\pi\\ &=\boxed{1{,}75\pi\ \text{m}\ \approx 5{,}497\ \text{m}} \end{aligned} \]

Tangentes a partir de um ponto externo

De um ponto \(P\) externo a uma circunferência de raio \(r=6\,\text{cm}\), traçam-se duas tangentes \(PA\) e \(PB\). Sabe-se que \(OP=10\,\text{cm}\) (centro \(O\)).

Dados: \(r=6\,\text{cm}\), \(OP=10\,\text{cm}\).

Qual é o comprimento de cada tangente \(PT\) (onde \(T\) é o ponto de tangência)?

Ver solução

\[ \begin{aligned} PT^2&=OP^2-r^2\\ &=10^2-6^2\\ &=100-36\\ &=64\\ PT&=\boxed{8\ \text{cm}} \end{aligned} \]

Erros comuns (e como evitar)

Confundir diâmetro com raio. Lembre: \(d=2r\).
Misturar graus e radianos. Para arco: em graus \(L=\dfrac{\alpha}{360^\circ}2\pi r\); em radianos \(L=r\theta\).
Usar Pitágoras fora de contexto. Para cordas, prefira \(c=2r\sin(\alpha/2)\) ou \(c=2\sqrt{r^2-x^2}\).

Para se aprofundar, veja comprimento da circunferência e área do setor circular.

Exercícios (múltipla escolha)

Corda por ângulo

Numa roda de raio \(r=9\,\text{cm}\), dois raios formam \(\alpha=80^\circ\).

O comprimento da corda é:

A) \(9\ \text{cm}\)
B) \( \mathbf{13{,}94\ \text{cm}} \)
C) \(14{,}50\ \text{cm}\)
D) \(15{,}00\ \text{cm}\)

Gabarito

\[ c=2r\sin\!\left(\frac{\alpha}{2}\right)=2\cdot 9\cdot \sin 40^\circ\approx 18\cdot 0{,}6428=\boxed{13{,}94\ \text{cm}}\ (\text{B}) \]

Corda por distância

Uma corda está a \(x=5\,\text{cm}\) do centro de uma circunferência de raio \(r=13\,\text{cm}\).

Seu comprimento é:

A) \(20\ \text{cm}\)
B) \( \mathbf{24\ \text{cm}} \)
C) \(26\ \text{cm}\)
D) \( \,2\sqrt{194}\ \text{cm}\, \)

Gabarito

\[ c=2\sqrt{r^2-x^2}=2\sqrt{13^2-5^2}=2\sqrt{169-25}=2\sqrt{144}=\boxed{24\ \text{cm}}\ (\text{B}) \]

Arco e comprimento

Um círculo tem diâmetro \(d=20\,\text{cm}\). Qual o comprimento do arco correspondente a \(\alpha=30^\circ\)?

Assinale a alternativa correta:

A) \( \mathbf{\tfrac{1}{12}\cdot 20\pi= \tfrac{5}{3}\pi\ \text{cm}} \)
B) \( \tfrac{1}{6}\cdot 20\pi \ \text{cm}\)
C) \( \tfrac{1}{8}\cdot 20\pi \ \text{cm}\)
D) \( \tfrac{1}{4}\cdot 20\pi \ \text{cm}\)

Gabarito

\[ L=\frac{\alpha}{360^\circ}\,2\pi r=\frac{30^\circ}{360^\circ}\cdot 2\pi\cdot 10=\frac{1}{12}\cdot 20\pi=\boxed{\tfrac{5}{3}\pi\ \text{cm}}\ (\text{A}) \]

Tangentes de um ponto

De um ponto \(P\) fora da circunferência com \(OP=13\,\text{cm}\) (centro \(O\)), traçam-se tangentes aos pontos \(A\) e \(B\) da circunferência de raio \(r=5\,\text{cm}\).

O comprimento \(PA\) é: