Cologaritmo: definição, fórmulas e exercícios

O cologaritmo é, essencialmente, o logaritmo do inverso de um número. Para base \(a\) (com \(a>0\) e \(a\neq1\)) e \(b>0\), definimos:
\( \displaystyle \mathrm{colog}_a(b)=\log_a\!\left(\frac{1}{b}\right) \;=\; -\,\log_a b \)
Quando usar?
O cologaritmo é útil para simplificações algébricas, manipulação de expressões com inversos e em demonstrações de propriedades. Ele aparece naturalmente quando aplicamos a regra do quociente ou lidamos com \(b^{-1}\).
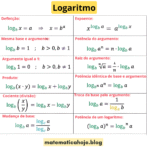
Propriedades rápidas
- Definição: \( \mathrm{colog}_a(b)=\log_a(1/b) \).
- Oposto do log: \( \mathrm{colog}_a(b)=-\log_a b \).
- Com potência: \( \mathrm{colog}_a(b^k)=-k\,\log_a b \).
- Com produto: \( \mathrm{colog}_a(xy)=-(\log_a x+\log_a y) \).
- Com quociente: \( \mathrm{colog}_a(x/y)=-(\log_a x-\log_a y) \).
Exemplos resolvidos
Exemplo 1 — \( \mathrm{colog}_{10}(100) \)
\( \mathrm{colog}_{10}(100)=-\log_{10}100=-2 \). (Porque \( \log_{10}100=2 \)).
Exemplo 2 — \( \mathrm{colog}_{2}(8) \)
\( \mathrm{colog}_{2}(8)=-\log_{2}8=-3 \), pois \(8=2^{3}\).
Exemplo 3 — \( \mathrm{colog}_{10}(0{,}01) \)
\( \log_{10}(0{,}01)=-2 \Rightarrow \mathrm{colog}_{10}(0{,}01)=-(-2)=2 \).
Exercícios (múltipla escolha)
1) \( \mathrm{colog}_{10}(1000)= \)
- a) \(-2\)
- b) \(-3\)
- c) \(2\)
- d) \(3\)
Ver solução
\( \log_{10}1000=3 \Rightarrow \mathrm{colog}_{10}(1000)=-3 \). Alternativa b.
2) Se \( \mathrm{colog}_{2}(4)=x \), então \(x=\)
- a) \(-2\)
- b) \(-1\)
- c) \(1\)
- d) \(2\)
Ver solução
\( \log_{2}4=2 \Rightarrow \mathrm{colog}_{2}(4)=-2 \). Alternativa a.
3) \( \mathrm{colog}_{3}(9)= \)
- a) \(-1\)
- b) \(-2\)
- c) \(2\)
- d) \(1\)
Ver solução
\( \log_{3}9=2 \Rightarrow \mathrm{colog}_{3}(9)=-2 \). Alternativa b.
4) O cologaritmo de \(b\) em base \(a\) é:
- a) \( (\log_a b)^2 \)
- b) \( 1/\log_a b \)
- c) Sem relação com logaritmos
- d) \( -\log_a b \)
Ver solução
Por definição, \( \mathrm{colog}_a(b)=-\log_a b \). Alternativa d.
Leituras relacionadas (interno/SEO)
- Propriedades dos logaritmos
- Reciprocidade dos logaritmos
- Propriedade fundamental \(a^{\log_a x}=x\)
- Mudança de base de um logaritmo
- Logaritmo natural (ln)
Materiais e produtos do blog
- Mapas mentais de Matemática
- ENEM Matemática
- Pacote com 10 eBooks
- Banco de questões de Matemática
- eBook de Fórmulas Matemáticas (recomendado para revisão rápida de logaritmos e cologaritmo)