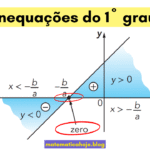
Como Construir o Gráfico da Função Afim
Este guia mostra, de forma objetiva, como traçar o gráfico da função afim (ou função polinomial de 1º grau) no plano cartesiano. Conteúdo essencial para ENEM, vestibulares e concursos.
1) Fórmula e elementos
- a — coeficiente angular (inclinação da reta: crescimento/decrescimento).
- b — coeficiente linear (intercepto em \(y\), ponto \( (0,b) \)).
2) Dois pontos básicos para traçar a reta
- Intercepto em \(y\): coloque \(x=0\) ⇒ \(f(0)=b\) ⇒ ponto \( (0,b) \).
- Zero da função: resolva \(f(x)=0\) ⇒ \(ax+b=0\) ⇒ \(x_0=-\dfrac{b}{a}\) Ponto \( (x_0,0) \) no eixo \(x\).
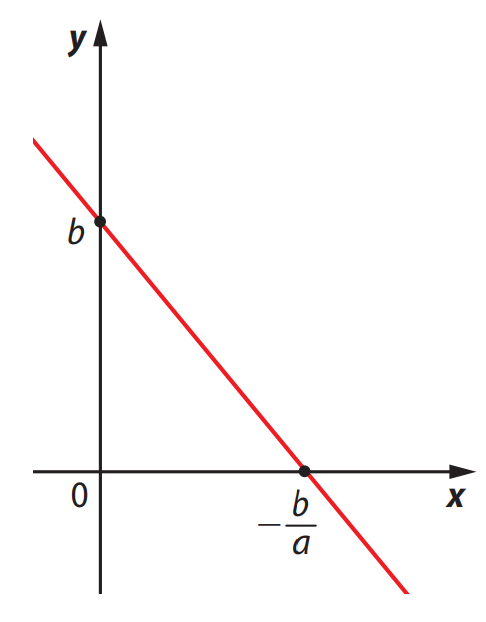
Com esses dois pontos já é possível traçar a reta.
3) Usando o coeficiente angular para checar a inclinação
A “inclinação” é a razão entre as variações: \( a=\dfrac{\Delta y}{\Delta x} \)
- \(a>0\) → reta crescente (sobe da esquerda para a direita).
- \(a<0\) → reta decrescente (desce da esquerda para a direita).
4) Casos especiais
- \(a=0\) ⇒ função constante \(f(x)=b\): reta horizontal.
- \(b=0\) ⇒ \(f(x)=ax\): reta que passa pela origem.
📘 Tenha todas as fórmulas à mão
Baixe o eBook Fórmulas Matemática para revisar rapidamente funções, geometria, estatística e muito mais. Ideal para provas e revisões.
Baixar eBook de Fórmulas5) Exemplo guiado (passo a passo)
Exemplo: Construa o gráfico de \(f(x)=-\;3x+6\).
Ver solução
Ponto no eixo \(y\):
\(f(0)=-3\cdot 0+6=6 \Rightarrow (0,6)\)
Zero da função:
\( -3x+6=0 \)
\( -3x=-6 \)
\( x=2 \Rightarrow (2,0) \)
Inclinação \(a=-3<0\) ⇒ reta decrescente. Trace a reta passando por \((0,6)\) e \((2,0)\).
6) Exemplo com uso do coeficiente angular
Exemplo: \(f(x)=\dfrac{1}{2}x-4\).
Ver solução
Ponto A no eixo \(y\): \(f(0)=-4 \Rightarrow (0,-4)\).
Usando \(a=\frac{1}{2}\): para \(\Delta x=2\) temos \(\Delta y=1\).
De \((0,-4)\) caminhe \(+2\) em \(x\) e \(+1\) em \(y\) ⇒ ponto \(B=(2,-3)\). Trace a reta \(AB\).
(Opcional) Zero: \( \frac{1}{2}x-4=0 \Rightarrow x=8 \Rightarrow (8,0)\).
7) Exercícios (com solução)
1) Trace o gráfico de \(f(x)=2x+1\) encontrando os dois pontos básicos.
Ver solução
\(f(0)=1 \Rightarrow (0,1)\)
\(2x+1=0 \Rightarrow x=-\frac{1}{2} \Rightarrow \left(-\frac{1}{2},0\right)\)
Reta crescente passando por esses pontos.
2) Para \(f(x)=-x-5\), determine o zero e diga se a reta é crescente ou decrescente.
Ver solução
\(-x-5=0 \Rightarrow -x=5 \Rightarrow x=5\)
\(a=-1<0\) ⇒ decrescente.
3) Em \(f(x)=4\), qual é o gráfico?
Ver solução
Função constante (\(a=0\)). Reta horizontal passando por \(y=4\).
4) Dada \(f(x)=ax+b\) com pontos \(P(1,3)\) e \(Q(5,11)\) no gráfico, determine \(a\) e \(b\) e trace a reta.
Ver solução
\(a=\dfrac{11-3}{5-1}=\dfrac{8}{4}=2\)
\(3=2\cdot 1 + b \Rightarrow b=1\)
\(f(x)=2x+1\). Pontos básicos: \((0,1)\) e \(\left(-\frac{1}{2},0\right)\).
5) Um serviço custa taxa fixa de R$ 30,00 mais R$ 7,50 por hora. Modele por função e indique os dois pontos básicos.
Ver solução
\(f(x)=7{,}50x+30\)
Ponto no eixo \(y\): \((0,30)\)
Zero: \(7{,}50x+30=0 \Rightarrow x=-4\) (ponto \((-4,0)\); útil para traçar a reta pela interseção com \(x\)).
Próximos passos
- Aprofunde-se em funções elementares e compare com a função quadrática.
- Pratique no nosso Banco de Questões para fixar os conceitos.