Derivadas de Ordem Superior
Entenda e aplique derivadas de 2ª, 3ª e n-ésima ordem. Para revisar a base, leia: Definição de Derivada, Regras de Derivação, Produto e Quociente, Função Exponencial e Funções Logarítmicas.
1) Definição e notação
Se \(f\) é derivável e \(f’\) também é derivável, definimos a derivada segunda por \(f”=(f’)’\). Recursivamente, \(f^{(n)}=\dfrac{d^n}{dx^n}f\) é a derivada n-ésima.
\(\displaystyle f”=\frac{d^2y}{dx^2},\qquad f^{(3)}=\frac{d^3y}{dx^3},\qquad f^{(n)}=\frac{d}{dx}\!\left[\frac{d^{\,n-1}y}{dx^{\,n-1}}\right]\)
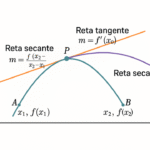
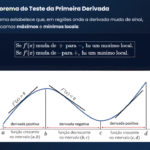
Geometricamente, \(f”\) se relaciona à concavidade e pontos de inflexão; ordens superiores surgem em séries de Taylor e em modelos de vibração/controle.
2) Fórmulas úteis
2.1 Regra do produto (Leibniz geral)
Se \(u,v\) são \(n\)-vezes deriváveis, então
\(\displaystyle \frac{d^n}{dx^n}[u\,v]=\sum_{k=0}^{n}\binom{n}{k}\,u^{(k)}\,v^{(n-k)}\).
Recupere as versões de 1ª ordem em produto e quociente.
2.2 Potências, exponenciais e logaritmos
\(\displaystyle \frac{d^n}{dx^n}\,[x^m]=m(m-1)\cdots(m-n+1)\,x^{m-n}\)
Para \(m\in\mathbb{N}\) e \(n>m\), a derivada é \(0\).
\(\displaystyle \frac{d^n}{dx^n}[a^x]=(\ln a)^n\,a^x\quad (a>0,\;a\neq1)\)
Relembre: função exponencial e funções logarítmicas.
3) Exemplos resolvidos
Exemplo A — Derivada segunda de um polinômio
\(f(x)=2x^3-9x\). Calcule \(f”(x)\).
Mostrar solução
\(f”(x)=(6x^2-9)’=12x\).
Resposta: \(f”(x)=12x\).
Exemplo B — Terceira derivada (misto)
\(f(x)=x^3-\cos x+e^x\). Encontre \(f^{(3)}(x)\).
Mostrar solução
\(f”(x)=6x+\cos x+e^x\).
\(f^{(3)}(x)=6-\sin x+e^x\).
Resposta final: \(\boxed{f^{(3)}(x)=6-\sin x+e^x}\)
Exemplo C — Produto com exponencial
\(f(x)=(x^2+1)\,e^{3x}\). Calcule \(f”(x)\) e \(f^{(3)}(x)\).
Mostrar solução
\(f”(x)=e^{3x}(9x^2+12x+11)\).
\(f^{(3)}(x)=e^{3x}(27x^2+54x+45)\).
Respostas: \(f”(x)=e^{3x}(9x^2+12x+11)\), \(f^{(3)}(x)=e^{3x}(27x^2+54x+45)\).
Exemplo D — Quociente com logaritmo
\(f(x)=\dfrac{\ln x}{x}\) (\(x>0\)). Encontre \(f”(x)\).
Mostrar solução
\(f'(x)=\dfrac{1-\ln x}{x^2}\).
\(f”(x)=\dfrac{2\ln x-3}{x^3}\).
Resposta: \(f”(x)=\dfrac{2\ln x-3}{x^3}\).
Exemplo E — Derivada n-ésima de \(2^x\)
Mostre que \(g^{(n)}(x)=(\ln2)^n\,2^x\), com \(g(x)=2^x\).
Mostrar solução
Conclusão: \(g^{(n)}(x)=(\ln2)^n 2^x\).
4) Tabela rápida
\(\displaystyle \frac{d^n}{dx^n}[e^{ax}]=a^n e^{ax}\)
\(\displaystyle \frac{d^n}{dx^n}[\sin(ax)]=a^n\sin\!\big(ax+n\pi/2\big)\)
\(\displaystyle \frac{d^n}{dx^n}[\cos(ax)]=a^n\cos\!\big(ax+n\pi/2\big)\)
\(\displaystyle \frac{d^n}{dx^n}[x^{-1}]=(-1)^n n!\,x^{-(n+1)}\)
5) Exercícios propostos
- Calcule \(f”(x)\) para \(f(x)=2x^3-9x\).
- Determine \(f^{(3)}(x)\) para \(f(x)=e^x\).
- Calcule \(f^{(4)}(x)\) para \(f(x)=\ln x\).
- Encontre \(f^{(5)}(x)\) para \(f(x)=2^x\).
- Encontre \(f^{(n)}(x)\) para \(f(x)=x^m\) (inteiro \(m\ge0\)).
6) Gabarito
Mostrar respostas
1) \(f”(x)=12x\).
2) \(f^{(3)}(x)=e^x\).
3) \(f^{(4)}(x)=6/x^4\).
4) \(f^{(5)}(x)=2^x(\ln2)^5\).
5) \(f^{(n)}(x)=m(m-1)\cdots(m-n+1)\,x^{m-n}\) (se \(n>m\), dá \(0\)).
Exercícios — Derivadas de Ordem Superior
Clique em Mostrar solução para abrir/fechar cada resolução detalhada. Observações de domínio foram incluídas quando necessário.
Parte 1 — Derivadas sucessivas simples
1. Calcule \(f”(x)\) para \(f(x)=3x^4-5x^2+2\).
Mostrar solução
\(f”(x)=36x^2-10\).
Resposta: \(36x^2-10\).
2. Determine \(f^{(3)}(x)\) para \(f(x)=x^3+2x^2-3x+1\).
Mostrar solução
\(f”(x)=6x+4\).
\(f^{(3)}(x)=6\).
Resposta: \(6\).
3. Encontre \(f”(x)\) para \(f(x)=e^{2x}\).
Mostrar solução
\(f”(x)=4e^{2x}\).
Resposta: \(4e^{2x}\).
4. Obtenha \(f^{(4)}(x)\) para \(f(x)=\cos(2x)\).
Mostrar solução
\(f”(x)=-4\cos(2x)\).
\(f^{(3)}(x)=8\sin(2x)\).
\(f^{(4)}(x)=16\cos(2x)\).
Resposta: \(16\cos(2x)\).
Parte 2 — Exponenciais e logarítmicas
5. Calcule \(g^{(5)}(x)\) para \(g(x)=2^x\).
Mostrar solução
Para \(a=2\): \(g^{(5)}(x)=(\ln 2)^5 2^x\).
Resposta: \((\ln 2)^5 2^x\).
6. Determine \(f”(x)\) para \(f(x)=\ln(x^2+1)\).
Mostrar solução
\(f”(x)=\dfrac{2(x^2+1)-4x^2}{(x^2+1)^2}=\dfrac{2-2x^2}{(x^2+1)^2}\).
Resposta: \(\dfrac{2(1-x^2)}{(x^2+1)^2}\).
14. Encontre \(f^{(3)}(x)\) para \(f(x)=x\ln x\).
Mostrar solução
\(f”(x)=1/x\).
\(f^{(3)}(x)=-1/x^2\).
Resposta: \(-x^{-2}\).
15. Obtenha \(f”(x)\) para \(f(x)=\dfrac{\sin x}{x}\).
Mostrar solução
\(f”(x)= -\dfrac{\sin x}{x}-\dfrac{2\cos x}{x^2}+\dfrac{2\sin x}{x^3}\).
Resposta: \(\dfrac{-x^2\sin x-2x\cos x+2\sin x}{x^3}\).