Distância de um ponto a uma reta

Distância de um ponto a uma reta — Fórmula e Exemplos Resolvidos

Distância de um Ponto a uma Reta — Fórmula, Definição e Exercícios

A distância de um ponto a uma reta é um dos conceitos mais importantes da Geometria Analítica. Ela representa o menor caminho possível entre um ponto e uma reta, medido ao longo de uma linha perpendicular à reta.

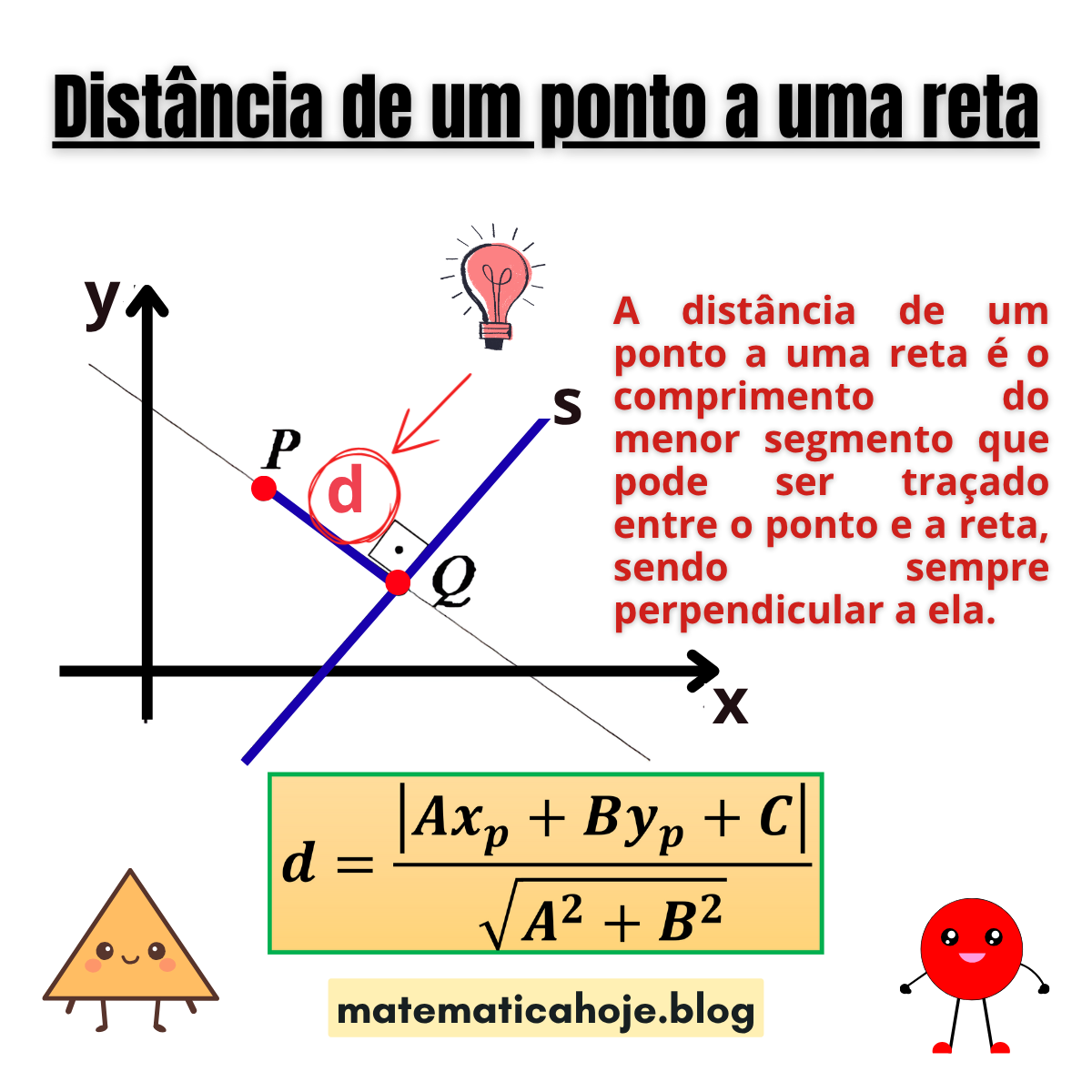
Distância de um ponto a uma reta - matematicaoje.blog

📘 O que é a Distância de um Ponto a uma Reta

Quando temos uma reta representada pela equação geral:

\( Ax + By + C = 0 \)

e um ponto \( P(x_p, y_p) \) fora dessa reta, a distância entre o ponto e a reta é o comprimento do segmento perpendicular traçado de \( P \) até a reta.

Essa distância é calculada pela fórmula:

\( d = \frac{|A x_p + B y_p + C|}{\sqrt{A^2 + B^2}} \)

Essa expressão fornece um valor sempre positivo, pois utiliza o módulo no numerador.

💡 O resultado indica a distância mínima entre o ponto e a reta, ou seja, o caminho mais curto entre ambos.

🧮 Interpretação Geométrica

A distância de um ponto a uma reta é medida ao longo da perpendicular que parte do ponto e toca a reta em apenas um ponto. Isso significa que, entre todos os possíveis segmentos que conectam o ponto à reta, a perpendicular é o menor deles.

Esse conceito é útil em problemas que envolvem posições relativas, como verificar se um ponto está acima, abaixo ou sobre uma reta.

📐 Exemplo 1

Exemplo: Determine a distância do ponto \( P(2, 3) \) à reta \( 2x + y – 5 = 0 \).

Substituindo na fórmula:

\( d = \frac{|2(2) + 1(3) – 5|}{\sqrt{2^2 + 1^2}} \)
\( d = \frac{|4 + 3 – 5|}{\sqrt{5}} = \frac{|2|}{\sqrt{5}} \)
\( \Rightarrow d = \frac{2}{\sqrt{5}} \approx 0{,}89 \)

📐 Exemplo 2

Exemplo: Calcule a distância entre o ponto \( P(-1, 4) \) e a reta \( 3x – 4y + 5 = 0 \).

Aplicando a fórmula:

\( d = \frac{|3(-1) – 4(4) + 5|}{\sqrt{3^2 + (-4)^2}} \)
\( d = \frac{|-3 – 16 + 5|}{\sqrt{25}} = \frac{|-14|}{5} \)
\( \Rightarrow d = \frac{14}{5} = 2{,}8 \)

📘 Aprenda TODAS as Fórmulas de Matemática em um só lugar!

Baixe o eBook Fórmulas Matemática e tenha acesso rápido às principais fórmulas de Geometria, Álgebra, Estatística e muito mais. Ideal para estudantes e concurseiros!

📥 Baixar o eBook Grátis

📚 Exercícios de Fixação

1. Calcule a distância do ponto \( P(1, 2) \) até a reta \( 3x + 4y – 6 = 0 \).

\( d = \frac{|3(1) + 4(2) – 6|}{\sqrt{3^2 + 4^2}} = \frac{|3 + 8 – 6|}{5} = \frac{5}{5} = 1 \)

2. Determine a distância do ponto \( P(-2, -1) \) à reta \( 2x – 3y + 6 = 0 \).

\( d = \frac{|2(-2) – 3(-1) + 6|}{\sqrt{2^2 + (-3)^2}} = \frac{|-4 + 3 + 6|}{\sqrt{13}} = \frac{5}{\sqrt{13}} \approx 1{,}39 \)

3 (Desafio). Qual é a distância do ponto \( P(5, -2) \) à reta \( 4x + 3y – 12 = 0 \)?

\( d = \frac{|4(5) + 3(-2) – 12|}{\sqrt{4^2 + 3^2}} = \frac{|20 – 6 – 12|}{5} = \frac{2}{5} = 0{,}4 \)

🔗 Continue Estudando

Relacionadas

Inclinação da Reta (Coeficiente Angular)

Retas Paralelas — Definição, Condições e Exemplos

Coeficiente Angular da Reta

"Artigo escrito por"

Adriano Rocha

Sou Adriano Rocha, professor de Matemática com mestrado e especialização em Resolução de Problemas, além de expertise em concursos públicos. Leciono no Colégio Estadual Mimoso do Oeste e utilizo metodologias inovadoras para aprimorar a compreensão matemática e a resolução de problemas. Produzo conteúdos como artigos para blogs, livros, eBooks e mapas mentais, além de desenvolver materiais didáticos e participar de eventos acadêmicos, sempre com o objetivo de contribuir para o ensino e aprendizagem da Matemática.