Domínio, contradomínio e imagem de uma Função
Conceitos fundamentais com exemplos visuais e questões comentadas.
Antes de avançar em funções, garanta a base em Conjuntos Numéricos. Para provas, veja também o guia do ENEM Matemática e o Banco de Questões.
Definições
Domínio
Conjunto de partida (entradas permitidas). Ex.: \(A=\mathbb{Z}\) ou \(A=\mathbb{R}\setminus\{2\}\).
Contradomínio
Conjunto de chegada possível. É definido junto com a função. Ex.: \(B=\mathbb{Z}\) ou \(B=\mathbb{R}\).
Imagem
Conjunto das saídas efetivamente obtidas: \(\mathrm{Im}(f)=\{\,f(x)\mid x\in A\,\}\). Sempre vale \(\mathrm{Im}(f)\subseteq B\).
Se \(\mathrm{Im}(f)=B\), a função é sobrejetora; se valores diferentes no domínio sempre geram valores diferentes, é injetora.
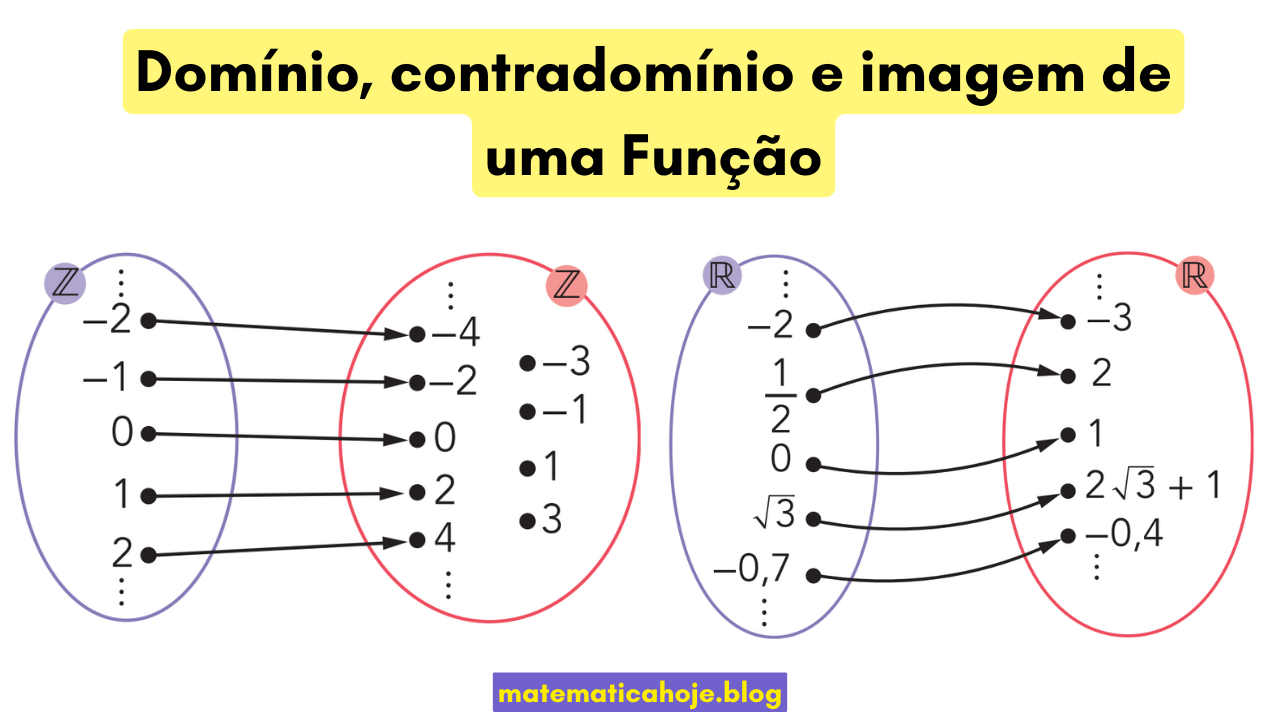
Exemplos da figura
1) \(f:\mathbb{Z}\to\mathbb{Z}\) com \(f(x)=2x\)
No diagrama da esquerda: \(-2\mapsto -4,\,-1\mapsto -2,\,0\mapsto 0,\,1\mapsto 2,\,2\mapsto 4\).
- Domínio: \(\mathbb{Z}\)
- Contradomínio: \(\mathbb{Z}\)
- Imagem dos mostrados: \(\{-4,-2,0,2,4\}\) (no geral, todos os pares).
2) \(g:\mathbb{R}\to\mathbb{R}\) com \(g(x)=2x+1\)
No diagrama da direita: \(-2\mapsto -3,\; \tfrac12\mapsto 2,\; 0\mapsto 1,\; \sqrt3\mapsto 2\sqrt3+1,\; -0{,}7\mapsto -0{,}4\).
- Domínio: \(\mathbb{R}\)
- Contradomínio: \(\mathbb{R}\)
- Imagem: \(\mathbb{R}\) (é sobrejetora e injetora — função afim crescente). Veja também equações do 1º grau.
Erros comuns
- Confundir imagem com contradomínio — a imagem é um subconjunto do contradomínio.
- Esquecer de declarar o domínio corretamente (ex.: restringir \(x\) para evitar divisão por zero ou raiz de número negativo).
- Tomar uma relação como função quando um mesmo \(x\) aparece ligado a dois \(y\).
Exercícios (com solução)
1) Considere \(f:\mathbb{Z}\to\mathbb{Z}\) dada por \(f(x)=2x\). Qual é a imagem do subconjunto \(\{-2,-1,0,1,2\}\)?
- \(\{-3,-1,0,1,3\}\)
- \(\{-4,-2,0,2,4\}\)
- \(\{-2,-1,0,1,2\}\)
- \(\{-5,-3,-1,1,3\}\)
Ver solução
\(f(-1)=-2\)
\(f(0)=0\)
\(f(1)=2\)
\(f(2)=4\)
Imagem: \(\{-4,-2,0,2,4\}\) ⇒ alternativa (b).
2) Para \(g:\mathbb{R}\to\mathbb{R}\), \(g(x)=2x+1\), calcule \(g(-2),\, g\!\left(\tfrac12\right),\, g(0),\, g(\sqrt3),\, g(-0{,}7)\).
- \(-3,\, 2,\, 1,\, 2\sqrt3+1,\,-0{,}4\)
- \(-5,\, 1,\, 0,\, 2\sqrt3-1,\,-1{,}4\)
- \(-1,\, 3,\, 1,\, 2\sqrt3+2,\, 0{,}3\)
- \(-3,\, 1,\, 1,\, 2\sqrt3+1,\,-0{,}4\)
Ver solução
\(g\!\left(\tfrac12\right)=2\cdot\tfrac12+1=2\)
\(g(0)=1\)
\(g(\sqrt3)=2\sqrt3+1\)
\(g(-0{,}7)=2(-0{,}7)+1=-0{,}4\)
Sequência: \(-3,\,2,\,1,\,2\sqrt3+1,\,-0{,}4\) ⇒ alternativa (a).
3) Qual afirmação é verdadeira?
- A imagem é sempre igual ao contradomínio.
- O domínio é igual ao contradomínio.
- A imagem é subconjunto do contradomínio.
- O domínio é subconjunto da imagem.
Ver solução
4) Para \(h:\mathbb{R}\to\mathbb{R}\) com \(h(x)=\sqrt{x-1}\), determine o domínio.
- \(\mathbb{R}\)
- \(x\ge 0\)
- \(x>1\)
- \(x\ge 1\)
Ver solução
5) Seja \(p:\mathbb{R}\to\mathbb{R}\), \(p(x)=\dfrac{1}{x-2}\). Assinale a opção que descreve domínio e imagem.
- Domínio: \(\mathbb{R}\); Imagem: \(\mathbb{R}\)
- Domínio: \(\mathbb{R}\setminus\{2\}\); Imagem: \(\mathbb{R}\setminus\{0\}\)
- Domínio: \(\mathbb{R}\setminus\{0\}\); Imagem: \(\mathbb{R}\setminus\{2\}\)
- Domínio: \((-\infty,2)\); Imagem: \((0,\infty)\)
Ver solução
\(\dfrac{1}{x-2}=0\) não ocorre ⇒ imagem exclui 0.
Portanto: Domínio \(\mathbb{R}\setminus\{2\}\), Imagem \(\mathbb{R}\setminus\{0\}\) ⇒ alternativa (b).
6) Em \(A=\{a,b\}\) e \(B=\{1,2,3\}\), a relação \(R=\{(a,1),(a,2),(b,3)\}\) é função?
- Sim, pois todo elemento de \(A\) tem imagem.
- Não, pois \(a\) possui duas imagens.
- Sim, pois o contradomínio tem três elementos.
- Não, pois \(b\) não tem imagem.
Ver solução
Para continuar estudando
- Mapas Mentais de Matemática
- Roteiro de Matemática para o ENEM
- Coleção 10 eBooks de Matemática
- Banco de Questões Matemática






















