ESFERA – Geometria Espacial
Volume, Área, Calota, Zona e Fuso (com exemplos e exercícios)
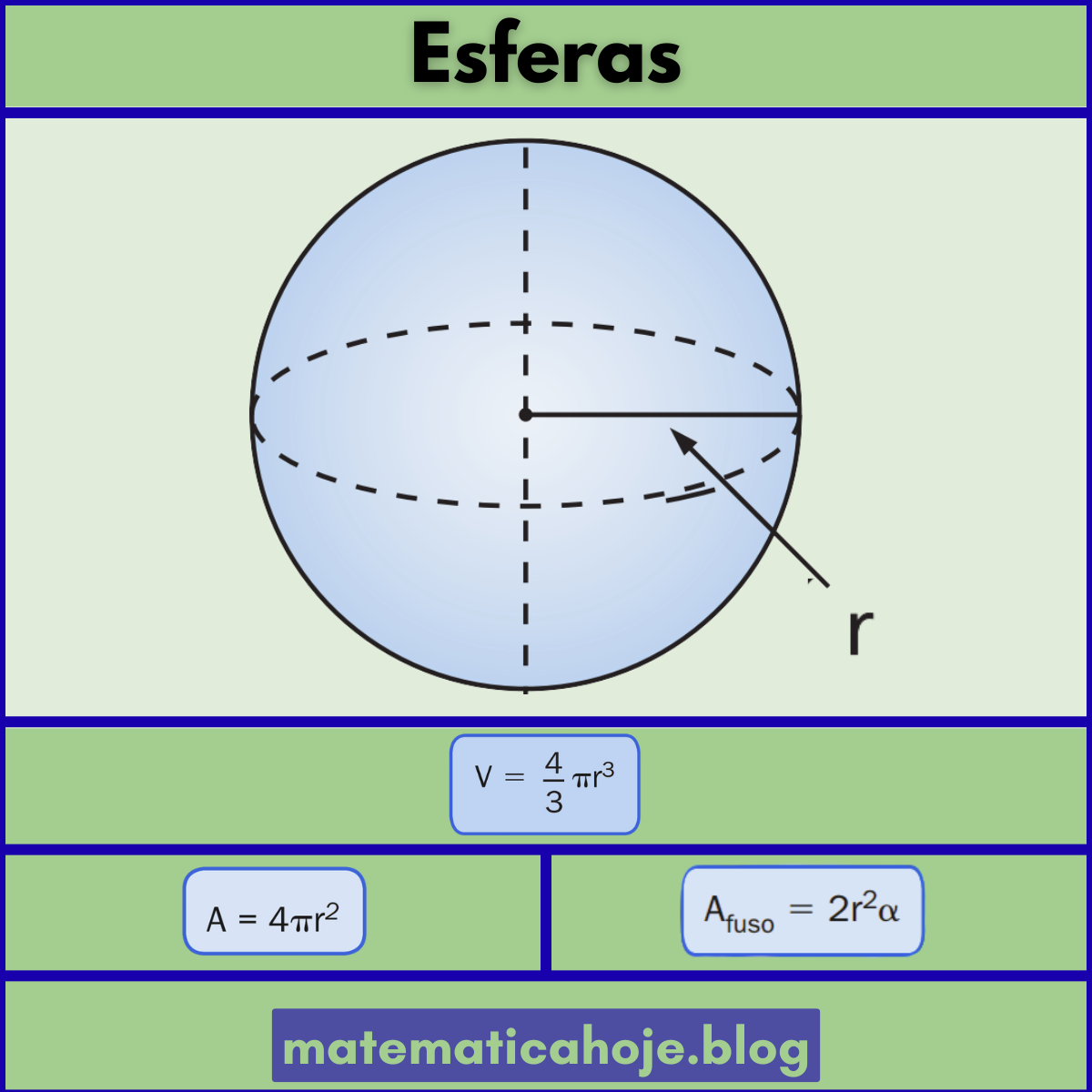
O que é uma esfera?
A esfera é o conjunto dos pontos do espaço a uma mesma distância \(r\) de um centro \(O\). Sua “casca” é a superfície esférica (área). Aparece em problemas de recipientes, astronomia e física.
🧠 Mapas Mentais de Matemática
📘 Banco de Questões
🎯 Guia do ENEM
📚 Coleção completa
📘 Fórmulas Principais
🔎 Casos Frequentes
Exemplo 1 (dados \(r\))
Calcule a área e o volume de uma esfera de raio \( r=5\,\text{cm} \).
📗 Baixe o eBook de Fórmulas Matemáticas
Todas as fórmulas (Álgebra, Geometria Espacial, Trigonometria…) em um único PDF para consulta rápida.
📥 Baixar AgoraExemplos Adicionais
Exemplo 2 (a partir da área). A área de uma esfera é \( A=144\pi\ \text{cm}^2 \). Determine o raio e o volume.
Exemplo 3 (calota). Numa esfera de raio \( r=10\,\text{cm} \), recorta-se uma calota de altura \( h=3\,\text{cm} \). Encontre \(A_{\text{calota}}\) e \(V_{\text{calota}}\).
Exercícios de Múltipla Escolha
1. (Volume) O diâmetro de uma esfera é \(12\,\text{cm}\). O volume é:
👀 Ver solução passo a passo
Gabarito: B.
2. (De volume para área) Uma esfera tem \( V=288\pi\ \text{cm}^3 \). A área da superfície é:
👀 Ver solução passo a passo
Gabarito: B.
3. (Calota/Zona) Em uma esfera de raio \( r=7\,\text{cm} \) recorta-se uma calota de altura \( h=4\,\text{cm} \). A área da calota é:
👀 Ver solução passo a passo
Gabarito: B.
Conclusão
Memorize: \(V=\tfrac{4}{3}\pi r^{3}\) e \(A=4\pi r^{2}\). Para recortes: \(A_{\text{calota}}=2\pi rh\), \(V_{\text{calota}}=\pi h^{2}\!\left(r-\tfrac{h}{3}\right)\), \(A_{\text{zona}}=2\pi rh\) e \(A_{\text{fuso}}=2r^{2}\alpha\) (com \(\alpha\) em radianos). Ótimo para provas e ENEM.