Esfera — Volume e Área (com Exercícios Resolvidos)
Tudo o que você precisa saber para acertar questões sobre esfera e hemisfério: fórmulas, ideias-chave, exemplos e uma lista de exercícios.
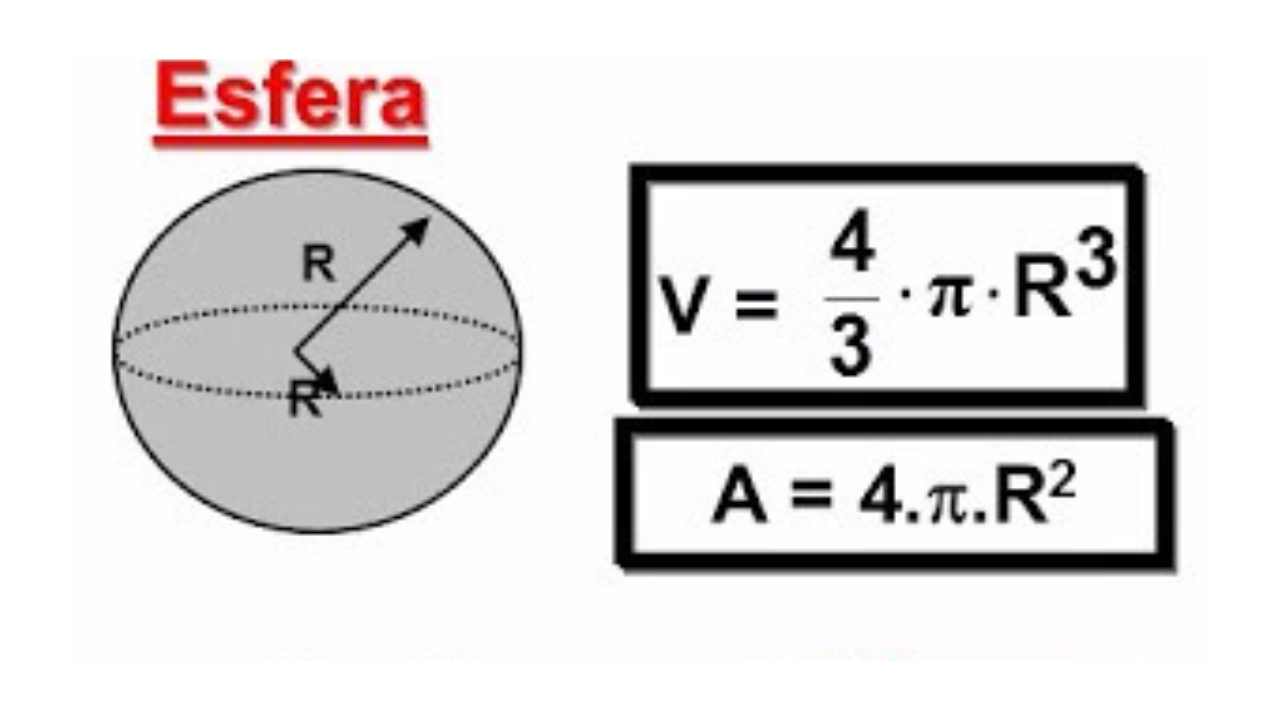
O que é uma Esfera?
A esfera é o conjunto de pontos do espaço equidistantes de um ponto fixo (o centro). Essa distância é o raio, indicado por R. O diâmetro vale D = 2R. A “casca” externa é a superfície esférica.
Aplicações: bolas, planetas, bolhas, rolamentos. Tema recorrente no ENEM Matemática e em concursos.
Fórmulas Essenciais
Volume e Área da Esfera (raio R)
Volume: \( V = \dfrac{4}{3}\,\pi R^3 \)
Área da superfície: \( A = 4\pi R^2 \)
Para o hemisfério (metade da esfera): \(V_{hemi}=\dfrac{2}{3}\pi R^3\). A área “curva” é \(2\pi R^2\); com a base circular incluída, \(A_{hemi,total}=3\pi R^2\).
Círculo Máximo
O maior “corte” plano numa esfera é um círculo de raio R (círculo máximo). Área: \( \pi R^2 \).
Reforce com os Mapas Mentais e pratique no Banco de Questões.
Exemplos Resolvidos
Exemplo 1 — Volume de uma bola
Enunciado. Uma bola tem diâmetro 12 cm. Calcule o volume.
Ver solução
Raio: \( R = \dfrac{12}{2} = 6 \) cm.
\( V = \dfrac{4}{3}\pi R^3 = \dfrac{4}{3}\pi\cdot 6^3 = \dfrac{4}{3}\pi\cdot 216 = \mathbf{288\pi\ \text{cm}^3} \) (≈ \(904.78\ \text{cm}^3\)).
Exemplo 2 — Raio a partir da área
Enunciado. A superfície de uma esfera mede \( 196\pi \) cm². Encontre R.
Ver solução
\( A = 4\pi R^2 = 196\pi \Rightarrow R^2 = 49 \Rightarrow R = \mathbf{7\ \text{cm}} \).
📘 eBook Grátis — Fórmulas Matemática
Todas as fórmulas de Geometria Espacial (esfera, cone, cilindro, prismas e pirâmides) e muito mais — perfeito para revisão.
➡️ Baixar AgoraExercícios Propostos
Resolva e confira o gabarito em cada questão. Quer mais listas? Acesse o Banco de Questões e a coleção 10 eBooks. Revise com os Mapas Mentais.
1) Uma esfera tem raio \( R=5 \) cm. Calcule: (a) o volume e (b) a área.
Ver solução
(b) \( A=4\pi 5^2=100\pi\ \text{cm}^2 \).
2) (Múltipla escolha) Dobrando o raio de uma esfera, o volume:
- duplica
- triplica
- quadruplica
- octuplica
Ver solução
3) A área de uma esfera é \( 324\pi \) cm². Determine o volume.
Ver solução
\( V=\frac{4}{3}\pi 9^3=\frac{4}{3}\pi 729=\mathbf{972\pi\ \text{cm}^3} \).
4) Um hemisfério de raio 6 cm será pintado apenas por fora (superfície curva). Qual a área pintada?
Ver solução
5) Uma esfera está inscrita em um cubo de aresta 10 cm. Calcule a diferença entre o volume do cubo e o volume da esfera.
Ver solução
Vcubo=\(10^3=1000\). Vesfera=\(\frac{4}{3}\pi 5^3=\frac{500\pi}{3}\).
Diferença: \(1000-\frac{500\pi}{3}\approx \mathbf{476{,}99\ \text{cm}^3}\).
6) (Múltipla escolha) A área da maior secção circular da esfera (círculo máximo) é:
- \( \pi R^2 \)
- \( 2\pi R^2 \)
- \( 3\pi R^2 \)
- \( 4\pi R^2 \)
Ver solução
7) Uma esfera metálica maciça tem raio 4 cm. É perfurada por um furo cilíndrico ao longo do diâmetro, de raio 2 cm. Determine o volume removido.
Ver solução
V = \( \pi r^2 h – 2\cdot \frac{1}{3}\pi r^2 H = \pi\cdot4\cdot8 – \frac{2}{3}\pi\cdot4\sqrt{12} \) = \( 32\pi – \frac{8\pi\sqrt{12}}{3} \) cm³. (Aproximado: \(32\pi – 9.237\pi \approx \mathbf{71.2\ \text{cm}^3}\)).
8) A diferença de volumes entre duas esferas concêntricas de raios 6 cm e 4 cm é:
Ver solução
9) A Terra tem raio médio \(R \approx 6371\) km. Estime a área de sua superfície (em milhões de km²).
Ver solução
10) (Teoria) Assinale a alternativa falsa:
- Se duas esferas têm o mesmo raio, têm o mesmo volume.
- O volume de uma esfera é proporcional ao cubo do raio.
- Ao triplicar o raio, a área triplica.
- O hemisfério tem área curva igual a \(2\pi R^2\).