Exercício Cunha Esférica — 15 questões com soluções

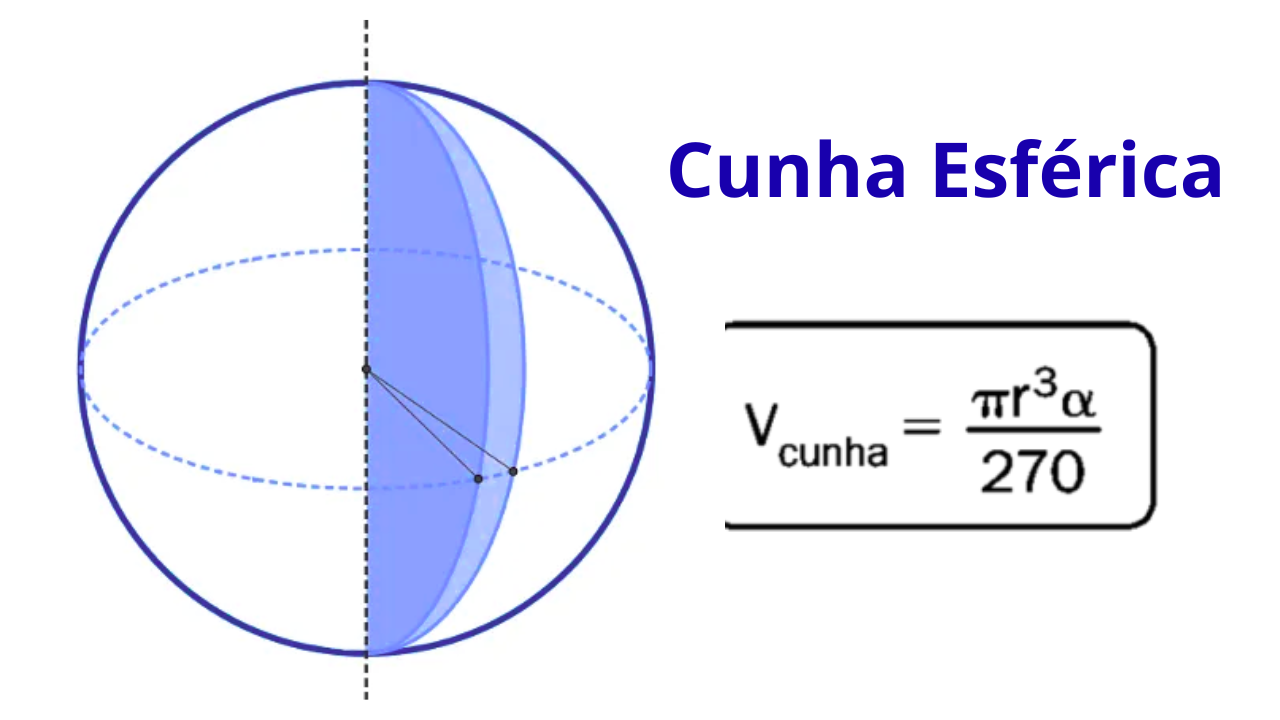
Cunha esférica: sólido correspondente a um fuso entre dois meridianos (ângulo α) na esfera de raio r — Cunha esférica (setor esférico) com ângulo central \(\alpha\) e esfera de raio \(r\).

O que os símbolos significam nos enunciados? Raio \(r\) é a distância do centro da esfera até a superfície; diâmetro \(d=2r\); ângulo central em graus \(\alpha\) (entre os meridianos que limitam a cunha); ângulo em radianos \(\theta\) (quando indicado). Quando houver aproximação, use \( \pi\approx 3{,}1416 \).

Fórmulas da cunha esférica (setor esférico)

Em graus \((\alpha)\): \( \displaystyle V_{\text{cunha}}=\frac{\pi r^{3}\alpha}{270} \)

Em radianos \((\theta)\): \( \displaystyle V_{\text{cunha}}=\frac{2}{3}\,\theta\,r^{3} \)

Área do fuso correspondente: \( \displaystyle A_{\text{fuso}}=\frac{\pi r^{2}\alpha}{90} = 2\theta r^{2}\)

Para revisar conceitos e ver mais exemplos gerais, consulte: Corpos redondos, Exercício Esfera, Cubo e Paralelepípedo.

1) Básico — volume direto. Numa esfera de raio \(r=3\ \text{cm}\), calcule o volume da cunha esférica cujo ângulo central é \(\alpha=60^\circ\).

\(5\pi\ \text{cm}^{3}\)
\(6\pi\ \text{cm}^{3}\)
\(8\pi\ \text{cm}^{3}\)
\(9\pi\ \text{cm}^{3}\)

Ver solução

\(V=\dfrac{\pi r^{3}\alpha}{270}\)

\(V=\dfrac{\pi\cdot 27\cdot 60}{270}\)

\(V=\pi\cdot \dfrac{1620}{270}=\boxed{6\pi\ \text{cm}^{3}}\)

Resposta: B.

2) Encontrando o ângulo. Em uma esfera de raio \(r=5\ \text{cm}\), a cunha tem volume \(V=\dfrac{500}{9}\pi\ \text{cm}^{3}\). Determine o ângulo \(\alpha\) (graus).

\(90^\circ\)
\(108^\circ\)
\(120^\circ\)
\(135^\circ\)

Ver solução

\(\dfrac{500}{9}\pi=\dfrac{\pi\cdot 125\cdot \alpha}{270}\Rightarrow \alpha=\dfrac{500\cdot 270}{9\cdot 125}=\boxed{120^\circ}\)

Resposta: C.

3) Em radianos. Considere uma esfera de raio \(r=2\ \text{m}\) e uma cunha com ângulo \(\theta=\dfrac{\pi}{4}\) (radianos). Calcule o volume.

\(\dfrac{\pi}{3}\ \text{m}^{3}\)
\(\dfrac{4\pi}{3}\ \text{m}^{3}\)
\(2\pi\ \text{m}^{3}\)
\(\dfrac{8\pi}{3}\ \text{m}^{3}\)

Ver solução

\(V=\dfrac{2}{3}\theta r^{3}=\dfrac{2}{3}\cdot\dfrac{\pi}{4}\cdot 8=\boxed{\dfrac{4\pi}{3}\ \text{m}^{3}}\)

Resposta: B.

4) Usando o diâmetro. Uma esfera tem diâmetro \(d=10\ \text{cm}\) (logo, raio \(r=5\ \text{cm}\)). Para \(\alpha=45^\circ\), determine o volume da cunha (forma exata).

\(\dfrac{125\pi}{9}\)
\(\dfrac{125\pi}{6}\)
\(\dfrac{250\pi}{9}\)
\(\dfrac{500\pi}{27}\)

Ver solução

\(V=\dfrac{\pi\cdot 125\cdot 45}{270}=\dfrac{125\pi}{6}\ \text{cm}^{3}\)

Resposta: B.

5) Hemisfério como caso particular. Para uma esfera de raio \(r=4\ \text{cm}\) e \(\alpha=180^\circ\), calcule o volume da cunha.

\(\dfrac{64\pi}{3}\)
\(\dfrac{96\pi}{3}\)
\(\dfrac{128\pi}{3}\)
\(64\pi\)

Ver solução

\(V=\dfrac{\pi r^{3}\alpha}{270}=\dfrac{\pi\cdot 64\cdot 180}{270}=\boxed{\dfrac{128\pi}{3}\ \text{cm}^{3}}\)

Resposta: C.

6) Encontrando o raio. Uma cunha tem volume \(V=100\pi\ \text{cm}^{3}\) e ângulo \(\alpha=30^\circ\). Qual é o raio da esfera \(r\) (aprox. em cm)?

8,80
9,20
9,65
10,00

Ver solução

\(100\pi=\dfrac{\pi r^{3}\cdot 30}{270}\Rightarrow r^{3}=100\cdot\dfrac{270}{30}=900\)

\(r=\sqrt[3]{900}\approx \boxed{9{,}65\ \text{cm}}\)

Resposta: C.

7) Comparando duas cunhas. Duas cunhas pertencem a esferas de raios \(r_A:r_B=2:3\) e ângulos \(\alpha_A=60^\circ\), \(\alpha_B=45^\circ\). A razão \(V_A:V_B\) vale:

\(16:27\)
\(32:81\)
\(8:27\)
\(64:81\)

Ver solução

\(V\propto r^{3}\alpha\Rightarrow (2^{3}\cdot 60):(3^{3}\cdot 45)=480:1215=\boxed{32:81}\)

Resposta: B.

8) Soma de dois setores. Numa esfera de raio \(r=6\ \text{cm}\), duas cunhas não sobrepostas possuem ângulos \(20^\circ\) e \(35^\circ\). Determine o volume total.

\(36\pi\)
\(40\pi\)
\(44\pi\)
\(48\pi\)

Ver solução

\(\alpha_{tot}=55^\circ\)

\(V=\dfrac{\pi r^{3}\alpha_{tot}}{270}=\dfrac{\pi\cdot 216\cdot 55}{270}=\dfrac{216}{270}\cdot 55\pi=\boxed{44\pi\ \text{cm}^{3}}\)

Resposta: C.

9) Achando \(\theta\). Em uma esfera de raio \(r=3\ \text{m}\), a cunha tem volume \(V=6\pi\ \text{m}^{3}\). Encontre o ângulo \(\theta\) em radianos.

\(\dfrac{\pi}{6}\)
\(\dfrac{\pi}{4}\)
\(\dfrac{\pi}{3}\)
\(\dfrac{\pi}{2}\)

Ver solução

\(\dfrac{2}{3}\theta r^{3}=6\pi\Rightarrow \dfrac{2}{3}\theta\cdot 27=6\pi\Rightarrow 18\theta=6\pi\Rightarrow \theta=\boxed{\dfrac{\pi}{3}}\)

Resposta: C.

10) Tanque esférico em litros. Um tanque esférico de raio \(r=1{,}5\ \text{m}\) contém uma cunha de \(\alpha=60^\circ\) preenchida com líquido. Calcule o volume em litros.

1 885 L
2 356 L
3 142 L
3 534 L

Ver solução

Exato: \(V=\dfrac{\pi r^{3}\alpha}{270}=\dfrac{\pi\cdot 3{,}375\cdot 60}{270}=0{,}75\pi\ \text{m}^{3}\)

Em litros: \(0{,}75\pi\times 1000\approx \boxed{2\,356\ \text{L}}\)

Resposta: B.

11) Proporção do volume total. O volume da esfera é 500 L. Qual deve ser o ângulo \(\alpha\) (graus) para que a cunha tenha 125 L?

\(60^\circ\)
\(75^\circ\)
\(90^\circ\)
\(120^\circ\)

Ver solução

\(\dfrac{\alpha}{360}=\dfrac{125}{500}=\dfrac{1}{4}\Rightarrow \alpha=\boxed{90^\circ}\)

Resposta: C.

12) Removendo um terço do volume. Qual \u>ângulo \(\alpha\) remove exatamente \(\dfrac{1}{3}\) do volume da esfera (mesmo \(r\))?

\(90^\circ\)
\(105^\circ\)
\(120^\circ\)
\(135^\circ\)

Ver solução

\(\alpha/360=1/3\Rightarrow \alpha=\boxed{120^\circ}\)

Resposta: C.

13) Comparação de dois ângulos em radianos. Em uma mesma esfera (mesmo \(r\)), compare os volumes das cunhas com \(\theta_1=\dfrac{\pi}{6}\) e \(\theta_2=\dfrac{\pi}{3}\).

\(V_2=V_1\)
\(V_2=1{,}5\,V_1\)
\(V_2=2\,V_1\)
\(V_2=3\,V_1\)

Ver solução

\(V\propto \theta\Rightarrow \dfrac{V_2}{V_1}=\dfrac{\pi/3}{\pi/6}=2\Rightarrow \boxed{V_2=2V_1}\)

Resposta: C.

14) Intervalo de ângulos possível. Em uma esfera de raio \(r=6\ \text{cm}\), deseja-se que o volume da cunha fique entre \(30\pi\) e \(40\pi\ \text{cm}^{3}\). Em qual intervalo de \(\alpha\) (graus) isso ocorre?

\(30^\circ\)–\(40^\circ\)
\(37{,}5^\circ\)–\(50^\circ\)
\(45^\circ\)–\(60^\circ\)
\(60^\circ\)–\(75^\circ\)

Ver solução

\(V=\dfrac{\pi\cdot 216\cdot \alpha}{270}=0{,}8\,\pi\,\alpha\)

\(30\pi\le 0{,}8\pi\alpha\le 40\pi\Rightarrow 37{,}5^\circ\le \alpha\le 50^\circ\)

Resposta: B.

15) Massa de uma peça de espuma. Uma peça em forma de cunha é moldada dentro de uma esfera de raio \(r=0{,}40\ \text{m}\), com ângulo \(\alpha=90^\circ\). A espuma tem densidade \(60\ \text{kg/m}^{3}\). Qual é a massa aproximada da peça?