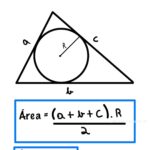
Fórmula de Heron: área do triângulo a partir dos três lados
Use o semiperímetro para calcular a área sem conhecer alturas — com teoria, exemplos e exercícios comentados.
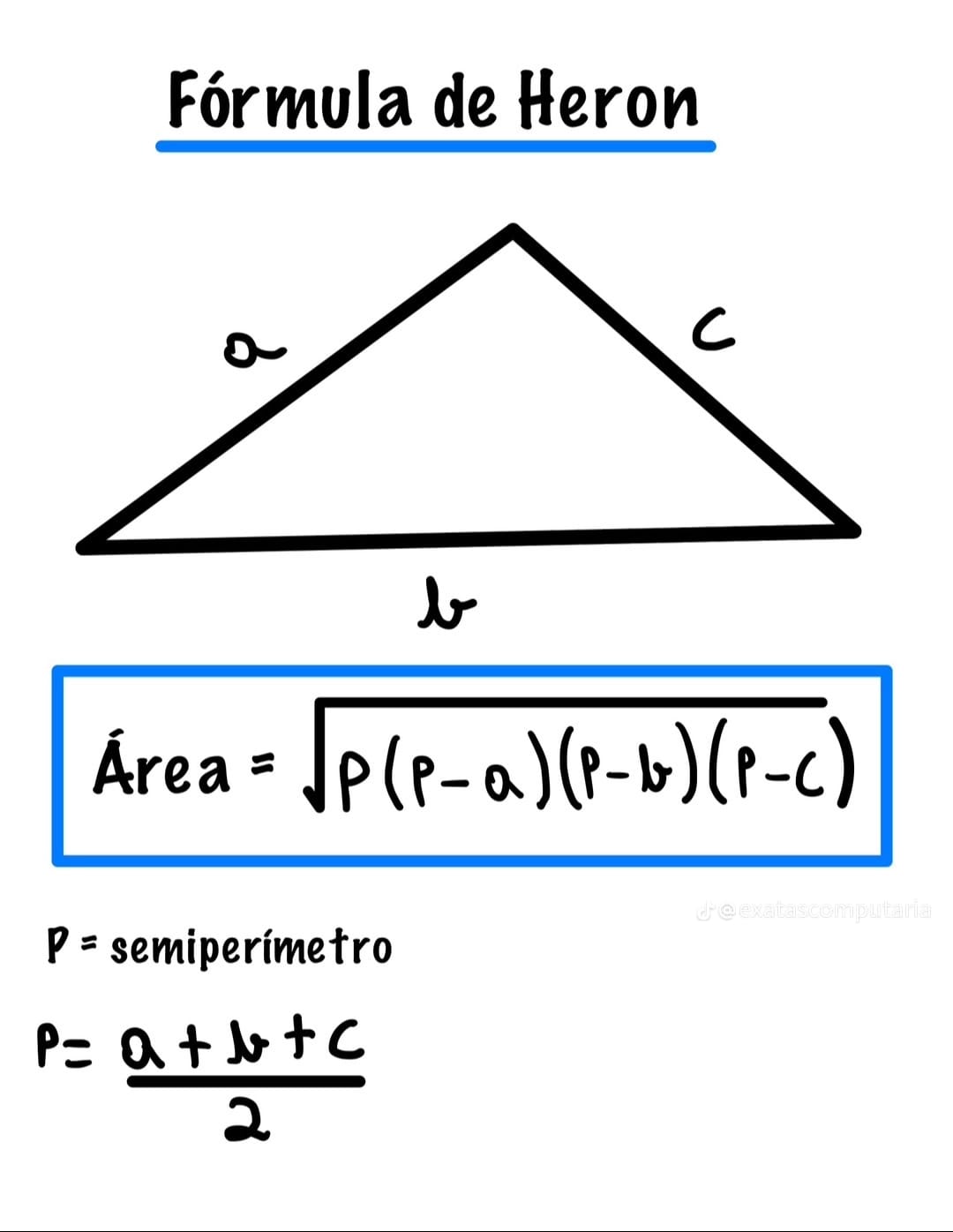
Enunciado da fórmula
Fórmula principal
\[ A=\sqrt{s(s-a)(s-b)(s-c)}\quad\text{com}\quad s=\frac{a+b+c}{2} \]
Válida para qualquer triângulo. Os resultados saem na unidade de área (cm², m², …).
Quando usar?
- Quando você conhece apenas os três lados \(a,b,c\).
- Quando não há altura ou ângulo entre dois lados disponível.
- Para verificar se um conjunto de lados forma triângulo (área real > 0).
Complete os estudos com: ENEM Matemática • Mapas Mentais • Banco de Questões
Outras formas de achar a área
Dependendo das informações do problema, é mais rápido usar:
\[ A=\frac{b\cdot h}{2}\quad(\text{base} \times \text{altura}) \]
\[ A=\frac{1}{2}\,a\,b\,\sin(\gamma)\quad(\text{ângulo entre } a \text{ e } b) \]
\[ A=\frac{a\,b\,c}{4R}\quad(\text{pelo circunrádio } R) \]
Veja também os artigos Área com seno e Área pelo circunrádio.
📘 Fórmulas sempre à mão
Ganhe tempo nas provas com o eBook Fórmulas Matemática — todas as fórmulas de Geometria, Trigonometria e muito mais.
Exemplos resolvidos
Exemplo 1 Clássico 3–4–5
Calcule a área do triângulo com lados \(a=3\), \(b=4\) e \(c=5\).
Ver solução
\(=6\).
\(A=\sqrt{s(s-a)(s-b)(s-c)}\)
\(=\sqrt{6\cdot (6-3)\cdot (6-4)\cdot (6-5)}\)
\(=\sqrt{6\cdot 3\cdot 2\cdot 1}\)
\(=\sqrt{36}\)
\(=6\).
Exemplo 2 Escaleno 7–8–9
Encontre a área do triângulo de lados \(7,8,9\).
Ver solução
\(=12\).
\(A=\sqrt{12\cdot (12-7)\cdot (12-8)\cdot (12-9)}\)
\(=\sqrt{12\cdot 5\cdot 4\cdot 3}\)
\(=\sqrt{720}\)
\(=12\sqrt{5}\approx 26{,}83\).
Exemplo 3 Isósceles 10–10–12
Calcule a área do triângulo isósceles com lados \(10,10,12\).
Ver solução
\(=16\).
\(A=\sqrt{16\cdot (16-10)\cdot (16-10)\cdot (16-12)}\)
\(=\sqrt{16\cdot 6\cdot 6\cdot 4}\)
\(=\sqrt{2304}\)
\(=48\).
Exercícios de múltipla escolha (com gabarito)
Enunciados completos e soluções com passos “um abaixo do outro”.
1) Determine a área (em unidades²) do triângulo com lados 3, 4 e 5.
Gabarito e solução
\(A=\sqrt{6\cdot 3\cdot 2\cdot 1}\)
\(=\sqrt{36}\)
\(=6\Rightarrow\) Letra C.
2) Calcule a área (aprox. em cm²) do triângulo de lados 7 cm, 8 cm e 9 cm.
Gabarito e solução
\(A=\sqrt{12\cdot 5\cdot 4\cdot 3}\)
\(=\sqrt{720}\)
\(\approx 26{,}83\Rightarrow\) Letra B.
3) Um triângulo isósceles tem lados 10 cm, 10 cm e 12 cm. A área é (em cm²):
Gabarito e solução
\(A=\sqrt{16\cdot 6\cdot 6\cdot 4}\)
\(=\sqrt{2304}\)
\(=48\Rightarrow\) Letra C.
4) Sabendo que a área de um triângulo é 24 cm² e dois lados medem 6 cm e 8 cm, qual valor do terceiro lado \(c\) torna verdadeira a Fórmula de Heron?
Gabarito e solução
\(A=\sqrt{12\cdot (12-6)\cdot (12-8)\cdot (12-10)}\)
\(=\sqrt{12\cdot 6\cdot 4\cdot 2}\)
\(=\sqrt{576}\)
\(=24\) (confere) \(\Rightarrow c=10\Rightarrow\) Letra B.
5) Num triângulo equilátero de lado 12 cm, calcule a área usando Heron.
Gabarito e solução
\(A=\sqrt{18\cdot 6\cdot 6\cdot 6}\)
\(=\sqrt{3888}\)
\(=36\sqrt3\Rightarrow\) Letra C.
6) Para o triângulo de lados 13, 14 e 15, determine a área.
Gabarito e solução
\(A=\sqrt{21\cdot (21-13)\cdot (21-14)\cdot (21-15)}\)
\(=\sqrt{21\cdot 8\cdot 7\cdot 6}\)
\(=\sqrt{7056}\)
\(=84\Rightarrow\) Letra C.
7) Para os lados 9, 10 e 17, qual é a área do triângulo?
Gabarito e solução
\(A=\sqrt{18\cdot (18-9)\cdot (18-10)\cdot (18-17)}\)
\(=\sqrt{18\cdot 9\cdot 8\cdot 1}\)
\(=\sqrt{1296}\)
\(=36\Rightarrow\) Letra C.
8) Um triângulo tem área 84 e dois lados valem 13 e 14. Qual é o terceiro lado?
Gabarito e solução
\(A=\sqrt{21\cdot 8\cdot 7\cdot 6}\)
\(=\sqrt{7056}\)
\(=84\) (confere) \(\Rightarrow c=15\Rightarrow\) Letra B.
Dicas finais
- Verifique a condição de existência: cada lado < soma dos outros dois.
- Se houver duas alternativas fáceis (ex.: triângulo retângulo), compare com \(A=\dfrac{b\cdot h}{2}\) para checar rápido.
- Para problemas com circunferência circunscrita, combine Heron com \(R=\dfrac{abc}{4A}\).