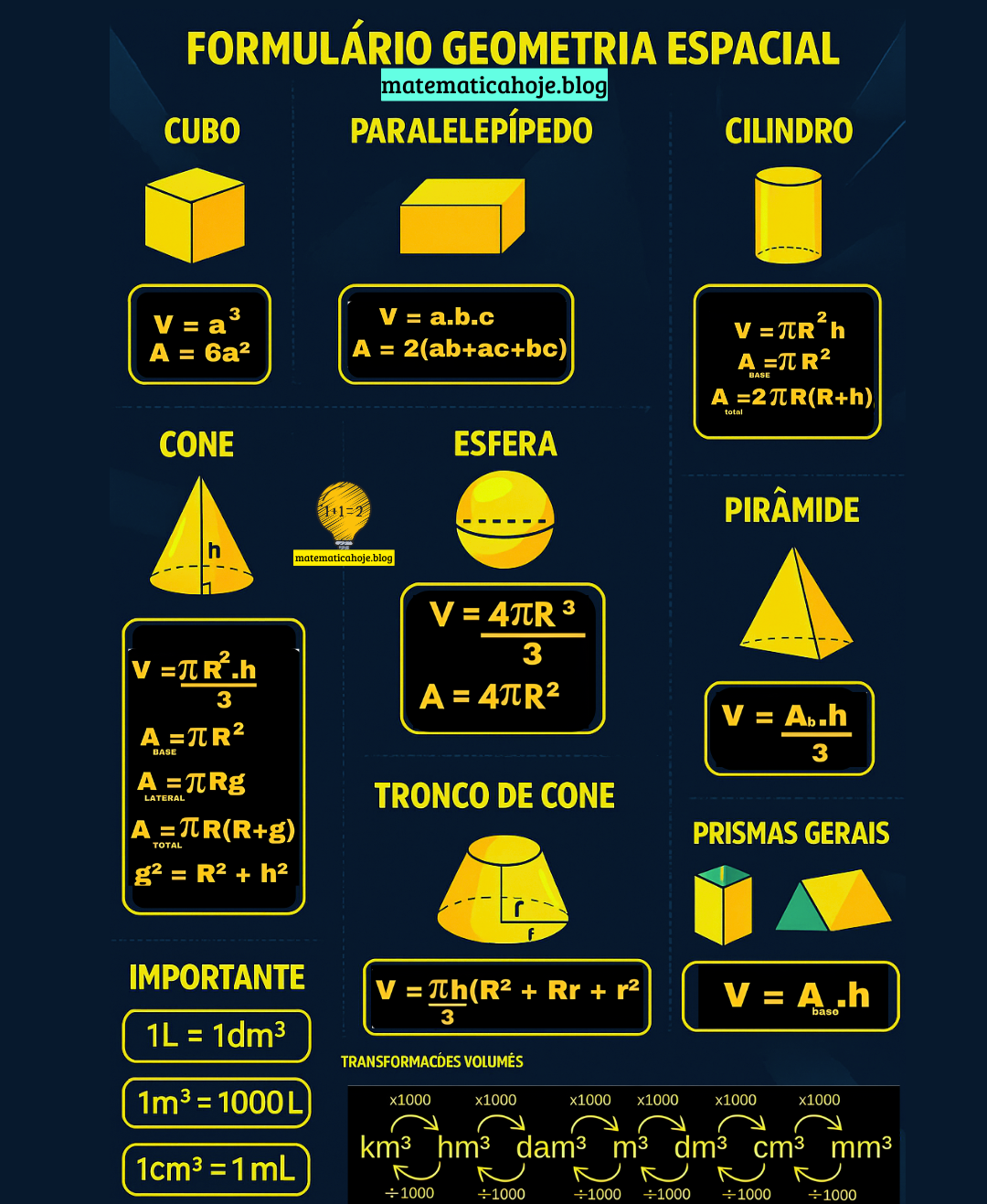
A geometria espacial cria um mapa em 3D do mundo: caixas, tubulações, piscinas, tanques, prédios, cones e até planetas podem ser explicados com ela. Se você está estudando para concursos, ENEM, vestibulares ou precisa revisar rapidamente para uma prova, dominar as fórmulas é o primeiro passo. Neste guia, você encontra um resumo completo das principais figuras geométricas, com explicações práticas, exemplos resolvidos linha a linha e uma lista final de exercícios com soluções escondidas para treinar. Para completar a experiência, o artigo inclui a imagem oficial a seguir, perfeita para salvar como resumo visual.
📘 Baixe gratuitamente o eBook de Fórmulas Matemáticas:
👉 Clique aqui para baixar
Fórmulas essenciais das figuras geométricas espaciais
1. Fórmulas do Cubo explicadas de forma simples
No cubo, todas as arestas têm o mesmo comprimento. Isso facilita muito os cálculos de área e volume.
Volume:
$$V = a^3$$
Área Total:
$$A = 6a^2$$
Exemplo prático
Um cubo tem aresta de 4 cm. Qual seu volume?
$$V = 4^3$$ = $$64\text{ cm}^3$$
2. Paralelepípedo: como calcular área e volume
O paralelepípedo é como uma “caixa de sapatos”. Suas faces têm formatos retangulares.
Volume:
$$V = a \cdot b \cdot c$$
Área Total:
$$A = 2(ab + ac + bc)$$
Exemplo prático
Uma caixa mede 5 cm × 3 cm × 2 cm. Qual é o volume?
$$V = 5 \cdot 3 \cdot 2$$ = $$30\text{ cm}^3$$
3. Cilindro: fórmulas que mais caem em provas
Volume:
$$V = \pi R^2 h$$
Área da base:
$$A_b = \pi R^2$$
Área Total:
$$A_t = 2\pi R (R + h)$$
Exemplo prático
Um cilindro tem raio 3 cm e altura 10 cm. Calcule o volume.
$$V = \pi \cdot 3^2 \cdot 10$$ = $$90\pi\text{ cm}^3$$
🧠 Mapa Mental de Geometria Espacial:
👉 Acesse aqui
4. Cone: volume, área e geratriz
Volume:
$$V = \frac{\pi R^2 h}{3}$$
Área lateral:
$$A_l = \pi R g$$
Área total:
$$A_t = \pi R (R+g)$$
Relação da geratriz:
$$g^2 = R^2 + h^2$$
Exemplo prático
Um cone tem raio 4 cm e geratriz 5 cm. Calcule a área lateral.
$$A_l = \pi \cdot 4 \cdot 5$$ = $$20\pi\text{ cm}^2$$
5. Esfera: volume e área mais cobrados
Volume:
$$V = \frac{4\pi R^3}{3}$$
Área:
$$A = 4\pi R^2$$
Exemplo prático
Uma bola tem raio 6 cm. Qual é a área da superfície?
$$A = 4\pi \cdot 6^2$$ = $$144\pi\text{ cm}^2$$
6. Pirâmide: o que mais aparece em concursos
Volume:
$$V = \frac{A_b \cdot h}{3}$$
Exemplo prático
Uma pirâmide tem base quadrada de lado 8 cm e altura 9 cm. Determine o volume.
$$A_b = 8^2 = 64$$ $$V = \frac{64 \cdot 9}{3}$$ = $$192\text{ cm}^3$$
7. Tronco de cone: fórmula completa
Volume:
$$V = \frac{\pi h (R^2 + Rr + r^2)}{3}$$
Exemplo prático
Um tronco de cone possui R = 6 cm, r = 2 cm e h = 10 cm.
$$V = \frac{\pi \cdot 10 (36 + 12 + 4)}{3}$$ = $$\frac{520\pi}{3}\text{ cm}^3$$
8. Prismas em geral: fórmula universal
Volume:
$$V = A_b \cdot h$$
Exemplo prático
Um prisma tem área da base 12 cm² e altura 7 cm. Qual o volume?
$$V = 12 \cdot 7$$ = $$84\text{ cm}^3$$
Conteúdos úteis para complementar:
Lista de Exercícios Resolvidos
Exercício 1
Qual o volume de um cilindro com R = 5 cm e h = 12 cm?
$$V = \pi R^2 h$$ $$V = \pi \cdot 5^2 \cdot 12$$ $$= \pi \cdot 25 \cdot 12$$ $$= 300\pi\text{ cm}^3$$
Exercício 2
Um cubo tem aresta 9 cm. Qual sua área total?
$$A = 6a^2$$ $$A = 6 \cdot 9^2$$ $$A = 6 \cdot 81$$ $$= 486\text{ cm}^2$$
Exercício 3
Calcule o volume de uma pirâmide com base 10 cm² e altura 15 cm.
$$V = \frac{A_b \cdot h}{3}$$ $$V = \frac{10 \cdot 15}{3}$$ $$V = 50\text{ cm}^3$$
Conclusão
A geometria espacial aparece em praticamente todas as provas de matemática, do ensino médio aos grandes concursos. Saber calcular áreas e volumes com segurança evita erros simples e aumenta sua precisão em questões de interpretação. Com os exemplos deste artigo, os exercícios resolvidos e o material extra do Matemática Hoje, você ganha domínio sobre as figuras mais cobradas e pode revisar rapidamente sempre que precisar.
FAQ
Quais fórmulas de geometria espacial mais caem em provas?
As mais cobradas são as de cilindro, cubo, paralelepípedo, esfera e pirâmide. Elas envolvem cálculos de volume, área lateral e área total. Saber identificar cada figura e substituir valores corretamente já resolve a maioria das questões.
Como estudar geometria espacial de forma eficiente?
O ideal é revisar fórmulas visualmente, praticar questões rápidas e treinar exercícios de concursos anteriores. Usar mapas mentais e resumos visuais ajuda muito na memorização e na aplicação prática durante as provas.
Onde posso encontrar mais exercícios de geometria?
O blog Matemática Hoje possui um Banco de Questões completo com exercícios de nível básico ao avançado, todos com soluções passo a passo para ajudar no aprendizado.
Autor: Adriano Rocha





















