Fórmulas do Cubo — área, volume e diagonais
Consulte as fórmulas principais do cubo (hexaedro regular) e veja exemplos resolvidos em formato vertical. Inclui área total, área de face, volume, diagonais e esferas inscrita e circunscrita.
1) O que é o cubo?
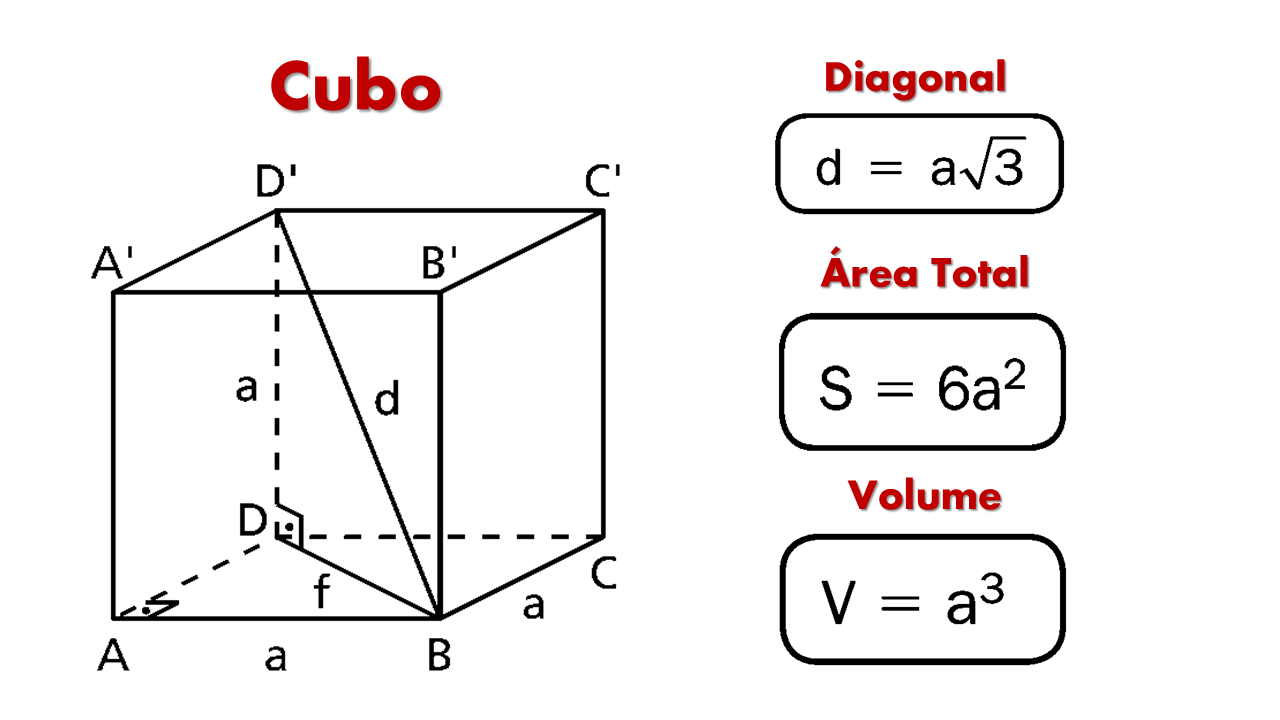
O cubo é um poliedro regular com 6 faces quadradas congruentes, 12 arestas e 8 vértices. Todas as arestas possuem o mesmo comprimento \(a\).
2) Formulário essencial do cubo
Áreas
- Área de uma face: \(A_{\text{face}}=a^2\)
- Área total: \(A_t=6a^2\)
- Área lateral (4 faces): \(A_l=4a^2\)
- Perímetro de uma face: \(P_{\text{face}}=4a\) | Comprimento total das arestas: \(12a\)
Volume
\(V=a^3\)
Diagonais
- Diagonal de face: \(d_f=a\sqrt{2}\)
- Diagonal espacial: \(d=a\sqrt{3}\)
Esferas relacionadas
- Esfera inscrita (tangente às faces): raio \(r=\dfrac{a}{2}\)
- Esfera circunscrita (passa pelos vértices): raio \(R=\dfrac{a\sqrt{3}}{2}\)
3) De onde vêm as fórmulas?
- Como a face é um quadrado de lado \(a\), \(A_{\text{face}}=a^2\) e \(A_t=6\cdot a^2\).
- O volume é “lado × lado × lado”: \(V=a\cdot a\cdot a=a^3\).
- Na diagonal de face, teorema de Pitágoras no quadrado: \(d_f=\sqrt{a^2+a^2}=a\sqrt{2}\).
- Na diagonal espacial, aplique Pitágoras no triângulo formado por \(d_f\) e a aresta \(a\): \(d=\sqrt{(a\sqrt{2})^2+a^2}=a\sqrt{3}\).
4) Exemplos resolvidos (contas na vertical)
-
Enunciado. Um cubo tem aresta \(a=7\ \text{cm}\). Calcule a área total e o volume.
Ver solução
Área total
$$\begin{aligned} A_t&=6a^2\\ &=6\cdot7^2\\ &=6\cdot49\\ &=\mathbf{294\ \text{cm}^2} \end{aligned}$$Volume
$$\begin{aligned} V&=a^3\\ &=7^3\\ &=7\cdot7\cdot7\\ &=49\cdot7\\ &=\mathbf{343\ \text{cm}^3} \end{aligned}$$ -
Enunciado. A diagonal espacial de um cubo mede \(d=12\ \text{cm}\). Calcule a aresta e o volume.
Ver solução
$$\begin{aligned} d&=a\sqrt{3}\\ a&=\dfrac{d}{\sqrt{3}}=\dfrac{12}{\sqrt{3}}\\ &=\dfrac{12\sqrt{3}}{3}\\ &=\mathbf{4\sqrt{3}\ \text{cm}}\\[6pt] V&=a^3=(4\sqrt{3})^3\\ &=64\cdot3\sqrt{3}\\ &=\mathbf{192\sqrt{3}\ \text{cm}^3} \end{aligned}$$Se preferir valor aproximado, \( \sqrt{3}\approx1{,}732\Rightarrow V\approx332{,}7\ \text{cm}^3 \).
-
Enunciado. Um presente em formato de cubo tem aresta \(a=0{,}3\ \text{m}\) e será embrulhado sem cobrir a face de baixo. Calcule a área de papel necessária.
Ver solução
$$\begin{aligned} A_l&=4a^2\\ &=4\cdot(0{,}3)^2\\ &=4\cdot0{,}09\\ &=\mathbf{0{,}36\ \text{m}^2} \end{aligned}$$ -
Enunciado. O raio da esfera circunscrita a um cubo é \(R=10\ \text{cm}\). Calcule a aresta do cubo e sua área total.
Ver solução
$$\begin{aligned} R&=\dfrac{a\sqrt{3}}{2}\\ a&=\dfrac{2R}{\sqrt{3}}=\dfrac{20}{\sqrt{3}}=\dfrac{20\sqrt{3}}{3}\\ A_t&=6a^2=6\left(\dfrac{20\sqrt{3}}{3}\right)^2\\ &=6\cdot\dfrac{400\cdot3}{9}\\ &=\dfrac{7200}{9}\\ &=\mathbf{800\ \text{cm}^2} \end{aligned}$$
5) Exercícios rápidos (gabarito em abre/fecha)
-
Um cubo tem \(a=5\ \text{cm}\). Calcule a diagonal de face e a diagonal espacial.
Gabarito
$$\begin{aligned} d_f&=a\sqrt{2}=5\sqrt{2}\ \text{cm}\\ d&=a\sqrt{3}=5\sqrt{3}\ \text{cm} \end{aligned}$$ -
O volume de um cubo é \(V=216\ \text{cm}^3\). Calcule a aresta e a área total.
Gabarito
$$\begin{aligned} a^3&=216\Rightarrow a=6\ \text{cm}\\ A_t&=6a^2=6\cdot36=\mathbf{216\ \text{cm}^2} \end{aligned}$$ -
Um cubo de aresta \(a\) tem esfera inscrita. Calcule o raio e o volume dessa esfera.
Gabarito
$$\begin{aligned} r&=\dfrac{a}{2}\\ V_{\text{esfera}}&=\dfrac{4}{3}\pi r^3=\dfrac{4}{3}\pi\left(\dfrac{a}{2}\right)^3 =\dfrac{\pi a^3}{6} \end{aligned}$$
6) Perguntas frequentes
| Qual a diferença entre diagonal de face e diagonal espacial? | Diagonal de face fica num quadrado da superfície \((a\sqrt{2})\). A diagonal espacial liga vértices opostos do cubo \((a\sqrt{3})\). |
|---|---|
| Como relacionar o cubo com esferas? | Inscrita: toca o centro das faces \((r=a/2)\). Circunscrita: passa pelos vértices \((R=a\sqrt{3}/2)\). |
| Planificação do cubo? | Seis quadrados congruentes; existem várias planificações válidas. |






















