(CESPE / CEBRASPE 2024 – ITAIPU BINACIONAL – Função: Técnico em Eletrônica)
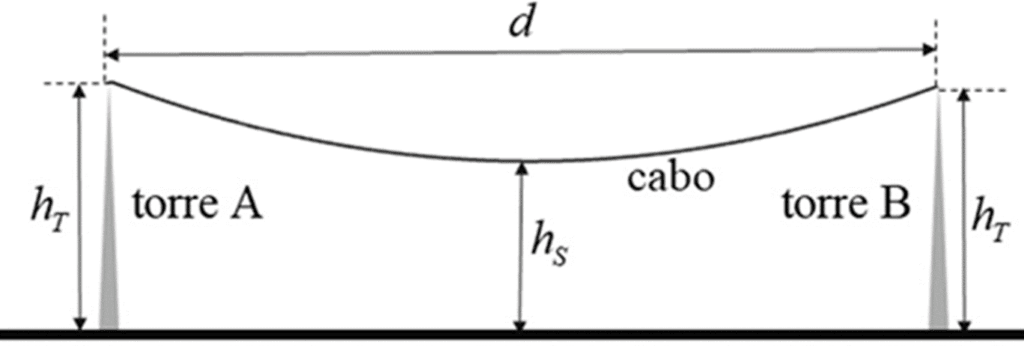
A figura precedente ilustra um trecho de um sistema de transmissão de energia elétrica em que: as torres A e B estão distantes de d = 150 m e suas alturas (hT) com relação ao solo são iguais a 20 m; um cabo elétrico está posicionado no topo das torres e a menor distância desse cabo ao solo é dada por hS = 15 m; o cabo descreve uma parábola f(d). Nessa situação, caso a distância entre as torres A e B fosse aumentada em 20%, o cabo continuasse a descrever a mesma parábola f(d), com a menor distância entre ele e o solo mantida igual a 15 m, e as alturas das torres A e B com relação ao solo fossem mantidas iguais entre elas, essas alturas passariam a ter valor, em metros, igual a
A) 21,0.
B) 22,2.
C) 24,0.
D) 26,0.
E) 27,2.
sse problema envolve o comportamento de uma parábola em um sistema de transmissão de energia elétrica, onde o cabo descreve a curva parabólica entre as torres A e B. Vamos analisar a situação e resolver o problema.
Passo 1: Definição da parábola original
A parábola pode ser descrita pela equação geral y(x) = ax2 + bx + c, onde:
- y(x) é a altura em relação ao solo.
- x é a posição horizontal.
Para o caso original:
- A menor distância do cabo ao solo é hS=15 metros, que ocorre no ponto médio entre as torres.
- As torres estão a uma distância d=150 metros, então a metade dessa distância é 75 metros.
Podemos posicionar a parábola com o vértice no ponto médio, ou seja, em x=75 metros. Nesse ponto, a altura é hS=15 metros. Nas extremidades x=0 e x=150 metros, as alturas são iguais a hT=20 metros.
Portanto, a função parabólica y(x) pode ser descrita por:
y(x)=a(x − 75)2 + 15
Sabemos que y(0) = 20 e y(150) = 20.
Passo 2: Determinação de a
Vamos usar y(0)=20:
20=a(0−75)2+15
20=5625a+15
a5 = 5625
a=1/1125
Agora que temos o valor de a, podemos descrever a parábola para qualquer distância entre as torres.
Agora que temos o valor de aaa, podemos descrever a parábola para qualquer distância entre as torres.
Passo 3: Aumento da distância entre as torres
Se a distância entre as torres A e B for aumentada em 20%, a nova distância entre as torres será:
dnova=150×1,2=180 metros
A nova posição do ponto médio será em x=90 metros.
Passo 4: Cálculo da nova altura das torres
A nova função parabólica será:
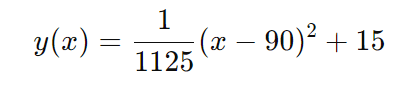
Precisamos encontrar a altura hT das torres, que correspondem às alturas nos pontos extremos x=0 e x=180:
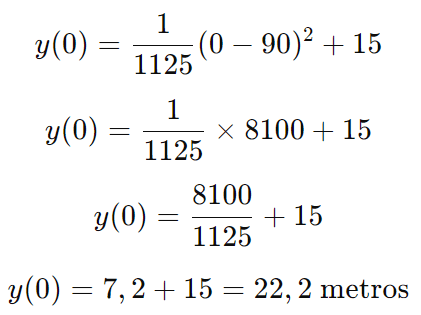
Portanto, as novas alturas das torres A e B serão de 22,2 metros.













