🚀 Crescimento e Decrescimento da Função Exponencial
A função exponencial está presente em diversos contextos do cotidiano e da ciência. Mas você sabia que o comportamento do gráfico dessa função muda conforme o valor da base?
Vamos explicar de forma clara como identificar quando a função exponencial é crescente e quando é decrescente, com base na forma geral:
$$ f(x) = a^x $$
🔎 O que é a função exponencial?
Chamamos de função exponencial qualquer função da forma:
$$ f(x) = a^x $$
com:
- \( a > 0 \)
- \( a \ne 1 \)
- \( x \in \mathbb{R} \)
O comportamento do gráfico depende exclusivamente do valor da base \( a \).
⬆️ Quando a função é crescente?
A função \( f(x) = a^x \) será crescente quando:
$$ a > 1 $$
• À medida que \( x \) aumenta, \( f(x) \) também aumenta.
• O gráfico sobe da esquerda para a direita.
• Exemplo: \( f(x) = 2^x \), \( f(x) = 3^x \), \( f(x) = e^x \)
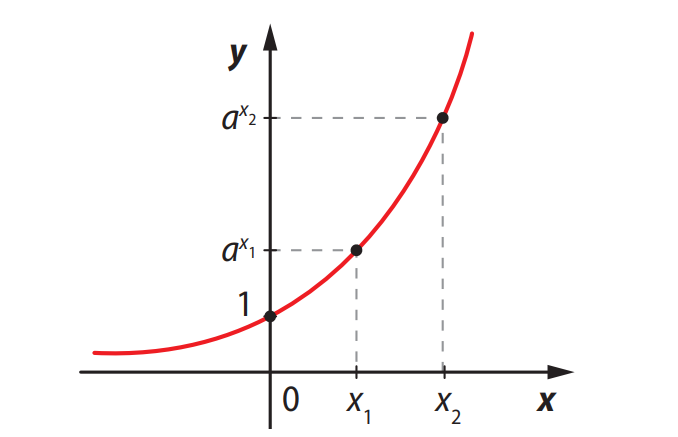
Gráfico de função exponencial com base \( a > 1 \)
⬇️ Quando a função é decrescente?
A função \( f(x) = a^x \) será decrescente quando:
$$ 0 < a < 1 $$
• À medida que \( x \) aumenta, \( f(x) \) diminui.
• O gráfico desce da esquerda para a direita.
• Exemplo: \( f(x) = \left(\frac{1}{2}\right)^x \), \( f(x) = 0{,}8^x \)

Gráfico de função exponencial com base \( 0 < a < 1 \)
📊 Comparação lado a lado
| Base \( a \) | Tipo de Gráfico | Comportamento |
|---|---|---|
| \( a > 1 \) | Crescente | Sobe da esquerda para a direita |
| \( 0 < a < 1 \) | Decrescente | Desce da esquerda para a direita |
📌 Propriedades importantes
- Domínio: \( \mathbb{R} \)
- Imagem: \( \mathbb{R}^+ \)
- Ponto fixo: \( f(0) = 1 \)
- O eixo x é assíntota horizontal
✅ Conclusão
Saber identificar se uma função exponencial é crescente ou decrescente é essencial para interpretar fenômenos reais como crescimento populacional, juros compostos e decaimento radioativo.
Resumo:
- Se \( a > 1 \), a função é crescente.
- Se \( 0 < a < 1 \), a função é decrescente.






















