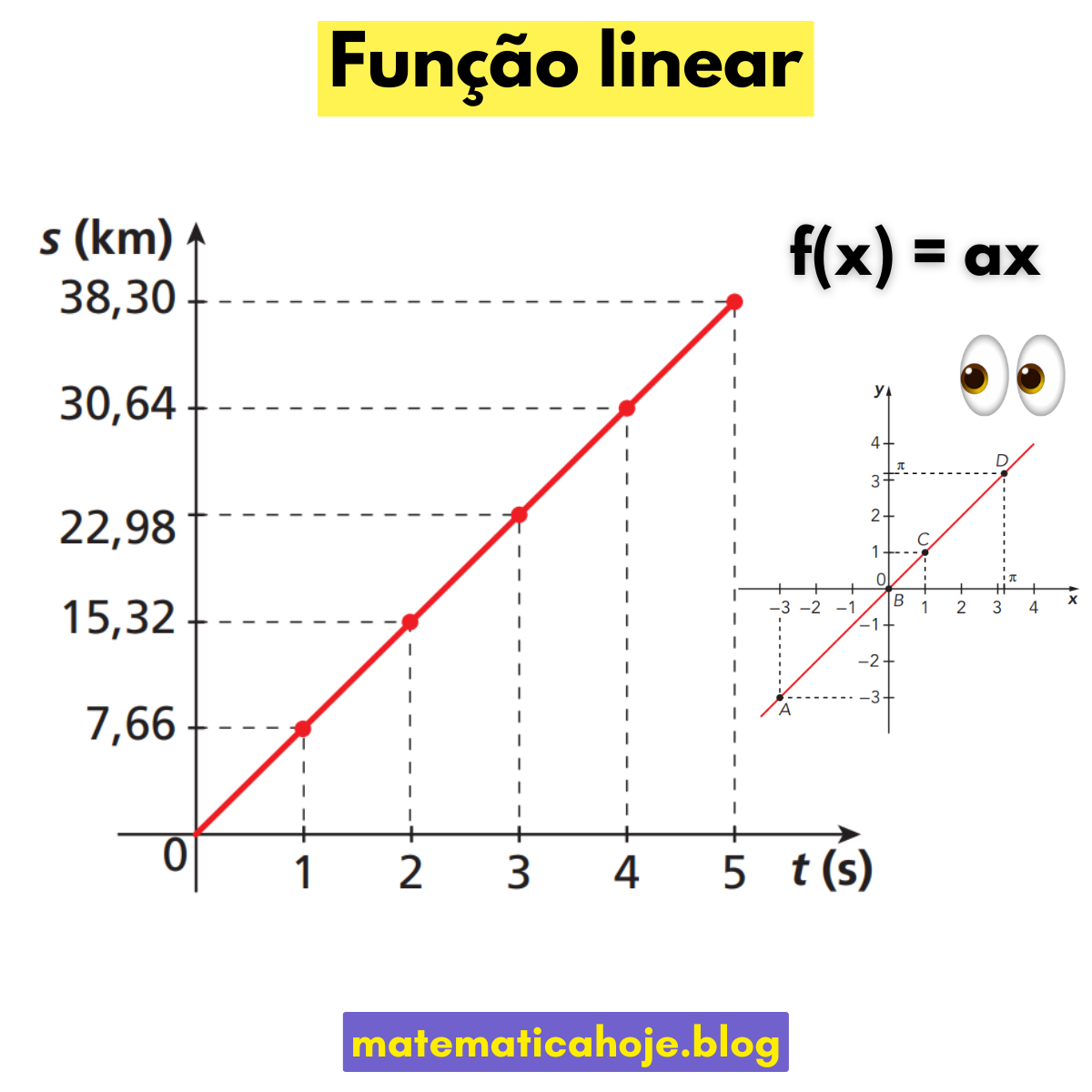
Função Linear f(x) = ax
A função linear é o caso especial da função afim em que o termo independente é zero. Seu estudo é base para problemas de proporcionalidade direta, inclinação de retas e movimento uniforme — conteúdos frequentes no ENEM e em concursos. Para uma visão geral de funções, veja Funções Matemáticas; e para o “próximo nível” compare com a Função Quadrática.
Definição e elementos
- Coeficiente angular \(a\): indica a inclinação (subida/descida) e também a razão constante \( \dfrac{f(x)}{x}=a \) (proporcionalidade direta).
- Gráfico: reta que passa pela origem \((0,0)\).
- Interseções: com os dois eixos ocorre no mesmo ponto \((0,0)\).
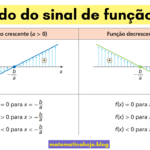
- Sinal: se \(a>0\), é crescente; se \(a<0\), é decrescente.
- Inversa: \(f^{-1}(x)=\dfrac{x}{a}\) (também linear).
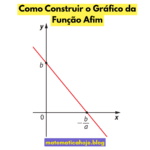
Como construir o gráfico
- Marque a origem \((0,0)\).
- Use a inclinação: para \(\Delta x=1\), mova \(\Delta y=a\). Assim encontra-se outro ponto e traça-se a reta.
- Opcional: faça uma tabela simples para confirmar.
\(x\) \(f(x)=ax\) 0 0 1 \(a\)
📘 Tenha as fórmulas sempre à mão
Baixe o eBook Fórmulas Matemática com resumos de funções, geometria e estatística. Ideal para revisões rápidas antes da prova.
Baixar eBook de FórmulasRelação com a Função Afim e com a Função Constante
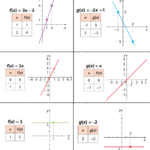
- Função afim: \(f(x)=ax+b\). A função linear é o caso \(b=0\). Veja também: Funções Matemáticas.
- Função constante: \(f(x)=b\) (inclinação nula). Compare os gráficos: a linear passa pela origem; a constante é horizontal.
Exemplos resolvidos
Exemplo 1 — Encontrar a lei pela razão constante. Em um movimento retilíneo uniforme, a distância (em km) é diretamente proporcional ao tempo (em h). Em 2 h, o móvel percorre 30,64 km. Determine a função \(s(t)\) e calcule \(s(5)\).
Ver solução
Sendo linear: \(s(t)=vt\). A razão \( \dfrac{s}{t} \) é constante: \(v=\dfrac{30,64}{2}=15,32\ \text{km/h}\).
\(s(t)=15,32\,t\). Logo, \(s(5)=15,32\cdot 5=76,6\ \text{km}\).
Exemplo 2 — A partir de dois pontos. Uma função linear passa por \((1,3)\) e \((4,12)\). Encontre \(a\) e a lei de \(f\).
Ver solução
\(a=\dfrac{12-3}{4-1}=\dfrac{9}{3}=3\). Assim, \(f(x)=3x\).
Exemplo 3 — Interpretação do sinal de \(a\). Para \(g(x)=-0{,}5x\), diga se a função é crescente ou decrescente e trace dois pontos.
Ver solução
\(a<0\) ⇒ decrescente. Pontos: \((0,0)\) e \((2,-1)\).
Exercícios (com solução no abre/fecha)
1) Uma função linear satisfaz \(f(3)=12\) e \(f(5)=20\). Encontre sua lei.
Ver solução
Como é linear: \(a=\dfrac{20-12}{5-3}= \dfrac{8}{2}=4\). Logo, \(f(x)=4x\).
2) Classifique como linear ou afim:
a) \(h(x)=7x\) b) \(p(x)=-2x+5\) c) \(q(x)=0\).
Ver solução
a) linear (b=0); b) afim não linear (b≠0); c) linear (a=0? — aqui é constante; por convenção, chama-se “função nula”, ainda passa pela origem).
3) Determine a inversa de \(f(x)=\dfrac{3}{2}x\) e verifique \(f^{-1}(f(x))=x\).
Ver solução
Troque \(x\leftrightarrow y\): \(x=\dfrac{3}{2}y \Rightarrow y=\dfrac{2}{3}x\). Logo \(f^{-1}(x)=\dfrac{2}{3}x\). Composição: \(\dfrac{2}{3}\cdot\dfrac{3}{2}x=x\).
4) Uma mangueira enche um reservatório a taxa constante de \(0{,}8\) m³/min. Modele o volume \(V(t)\) (em m³) após \(t\) minutos, considerando \(V(0)=0\). Quanto haverá após 25 min?
Ver solução
\(V(t)=0{,}8\,t\). Em 25 min: \(V(25)=0{,}8\cdot 25=20\) m³.
5) Dada \(r(x)=ax\) com \(a\neq 0\), mostre que a reta é sempre perpendicular ao eixo \(x\)?
Ver solução
Não é verdadeiro: a reta faz ângulo \(\theta\) com o eixo \(x\) tal que \(\tan\theta=a\). Só é perpendicular quando \(\theta=90^\circ\), o que não ocorre para retas de função linear (seria \(x=c\)).
Continue seus estudos
- Funções Matemáticas (visão geral)
- Banco de Questões de Matemática
- Compare com a Função Quadrática e com a Função Afim e Constante.
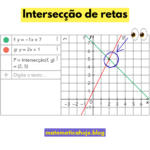
- Veja também artigos práticos de gráficos e interseções de retas no blog.