Conteúdo: Funções algébricas – Expressões em função de uma variável
Questão 03. O retângulo representado na figura tem lados que medem \( x \) e \( 2x \).
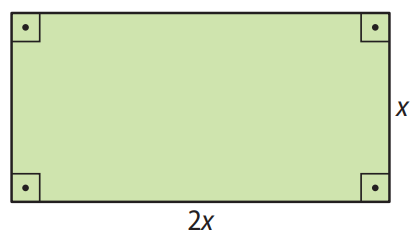
Expresse o perímetro \( P \), a área \( A \) e a medida \( d \) da diagonal desse retângulo em função de \( x \).
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
O retângulo possui base igual a \( 2x \) e altura igual a \( x \). Vamos usar fórmulas conhecidas de geometria para expressar as grandezas pedidas em função de \( x \).
1) Perímetro:
A fórmula do perímetro de um retângulo é:
$$ P = 2 \cdot (2x + x) = 2 \cdot 3x = \mathbf{6x} $$
2) Área:
A fórmula da área de um retângulo é:
$$ A = 2x \cdot x = \mathbf{2x^2} $$
3) Diagonal:
Aplicando o Teorema de Pitágoras:
$$ d = \sqrt{(2x)^2 + x^2} = \sqrt{4x^2 + x^2} = \sqrt{5x^2} = \mathbf{x\sqrt{5}} $$
✅ Conclusão:
- Perímetro: \( P = 6x \)
- Área: \( A = 2x^2 \)
- Diagonal: \( d = x\sqrt{5} \)




























