As funções exponenciais estão presentes em diversas situações do nosso dia a dia: no crescimento de uma população bacteriana, no rendimento mensal de uma aplicação financeira, na propagação de vírus ou até na depreciação de equipamentos. Compreender esse tipo de função é essencial para interpretar fenômenos reais que envolvem crescimento ou decaimento em ritmo acelerado.
Nesta série de questões, você será desafiado a aplicar seus conhecimentos sobre exponenciais em diferentes contextos, interpretando tabelas, gráficos, e leis matemáticas. Os exercícios envolvem:
- Construção e análise de gráficos;
- Identificação de funções crescentes e decrescentes;
- Interpretação de situações financeiras;
- Análise populacional com base em temperatura;
- Modelagem matemática com base em dados reais e fictícios.
Prepare-se para explorar como a Matemática descreve o mundo com precisão e profundidade. Vamos nessa?
🧠 Mapas Mentais de MatemáticaQuestão 19. Identifique como crescente ou decrescente as funções exponenciais definidas a seguir:
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Devemos classificar as funções exponenciais como crescente ou decrescente. Para isso, devemos analisar a base da potência e o sinal do expoente.
1) Lembrete teórico:
Uma função exponencial \( f(x) = a^x \):
– É crescente se \( a > 1 \)
– É decrescente se \( 0 < a < 1 \)
– Se a base é invertida por um expoente negativo, também resulta em função decrescente.
2) Analisando cada item:
- a) \( f(x) = 5^x \) → base \( > 1 \) → crescente
- b) \( f(x) = \left(\frac{1}{6}\right)^x \) → base \( < 1 \) → decrescente
- c) \( f(x) = 2^{-x} \) → \( 2^{-x} = \left(\frac{1}{2}\right)^x \) → base \( < 1 \) → decrescente
- d) \( f(x) = 3^{x/2} \) → base \( > 1 \), e expoente linear positivo → crescente
✅ Conclusão:
- a) Crescente
- b) Decrescente
- c) Decrescente
- d) Crescente
20. Esboce o gráfico das funções definidas a seguir. Depois, determine o domínio e a imagem de cada uma delas.
- \( f(x) = 3^x \)
- \( f(x) = 2^{x+1} \)
- \( f(x) = \left(\dfrac{1}{3}\right)^x \)
- \( f(x) = 2^x + 1 \)
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Para cada função exponencial, devemos:
– Identificar o domínio: valores de \( x \) permitidos;
– Determinar a imagem: os valores que \( f(x) \) pode assumir;
– Considerar o esboço do gráfico como apoio visual.
a) \( f(x) = 3^x \)
- Tipo: Função exponencial crescente.
- Domínio: \( \mathbb{R} \) (qualquer valor real pode ser usado como expoente).
- Imagem: \( \mathbb{R}_+^* \), ou seja, todos os reais positivos, sem incluir o zero.
b) \( f(x) = 2^{x+1} \)
- Tipo: Exponencial crescente, com deslocamento horizontal.
- Domínio: \( \mathbb{R} \)
- Imagem: \( \mathbb{R}_+^* \)
c) \( f(x) = \left(\dfrac{1}{3}\right)^x \)
- Tipo: Função exponencial decrescente (base entre 0 e 1).
- Domínio: \( \mathbb{R} \)
- Imagem: \( \mathbb{R}_+^* \)
d) \( f(x) = 2^x + 1 \)
- Tipo: Exponencial crescente com translação vertical de +1.
- Domínio: \( \mathbb{R} \)
- Imagem: \( \{y \in \mathbb{R} \mid y > 1\} \)
✅ Conclusão:
- a) Domínio: \( \mathbb{R} \); Imagem: \( \mathbb{R}_+^* \)
- b) Domínio: \( \mathbb{R} \); Imagem: \( \mathbb{R}_+^* \)
- c) Domínio: \( \mathbb{R} \); Imagem: \( \mathbb{R}_+^* \)
- d) Domínio: \( \mathbb{R} \); Imagem: \( \{y \in \mathbb{R} \mid y > 1\} \)
21. Durante a aula de Matemática, o professor comentou sobre uma função que representava o crescimento de uma população de bactérias e escreveu na lousa \( f(t) = 2^t \), para \( t \geq 0 \), em que \( t \) é dado em horas e \( f(t) \) em milhares de bactérias.
Um estudante distraído copiou \( f(t) = 2t \) e, portanto, seus cálculos não deram certo.
- Esboce os gráficos das duas funções em um mesmo sistema de coordenadas.
- Observando os gráficos construídos no item a, existe algum valor de \( t \) para o qual as duas funções assumem valor igual? Se sim, qual(is)?
- O que você pode concluir sobre o crescimento dessas duas funções?
- Para \( t = 3 \) h, qual é a diferença entre o número de bactérias nas duas funções?
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Duas funções foram dadas:
- Função correta: \( f(t) = 2^t \) – exponencial (crescimento acelerado)
- Função copiada: \( f(t) = 2t \) – linear (crescimento constante)
a) Esboço dos gráficos:
Ambas começam em \( f(0) = 1 \), mas a função exponencial cresce mais rapidamente com o tempo. No gráfico:
- \( 2^0 = 1 \), \( 2^1 = 2 \), \( 2^2 = 4 \), \( 2^3 = 8 \), …
- \( 2 \cdot 0 = 0 \), \( 2 \cdot 1 = 2 \), \( 2 \cdot 2 = 4 \), \( 2 \cdot 3 = 6 \), …
b) Valores iguais:
As funções coincidem quando seus valores são iguais:
- Para \( t = 1 \): \( 2^1 = 2 \) e \( 2 \cdot 1 = 2 \)
- Para \( t = 2 \): \( 2^2 = 4 \) e \( 2 \cdot 2 = 4 \)
Resposta: Sim, para \( t = 1 \) e \( t = 2 \)
c) Conclusão sobre o crescimento:
Ambas as funções são crescentes, porém:
- A função linear cresce de forma constante.
- A função exponencial cresce mais rapidamente à medida que o tempo aumenta.
Conclusão: Ambas são crescentes, mas a exponencial cresce mais rápido.
d) Diferença para \( t = 3 \):
– \( f_{\text{exponencial}}(3) = 2^3 = 8 \) (milhares de bactérias)
– \( f_{\text{linear}}(3) = 2 \cdot 3 = 6 \) (milhares de bactérias)
– Diferença: \( 8 – 6 = 2 \) mil = 2000 bactérias
✅ Resumo final:
- b) Sim, valores iguais para \( t = 1 \) e \( t = 2 \)
- c) Ambas são crescentes, mas a exponencial cresce mais rápido
- d) Diferença para \( t = 3 \): 2000 bactérias
22. Uma amostra de bactérias foi estudada quanto ao seu crescimento e decréscimo populacional \( P \), em centenas de milhares, em relação ao aumento da temperatura \( t \), em °C. Nesse experimento, a temperatura foi aumentada progressivamente, partindo de 0 °C e terminando em 120 °C, em um período de 24 horas. Observe, a seguir, a tabela e o gráfico que descrevem a variação populacional dessa amostra.
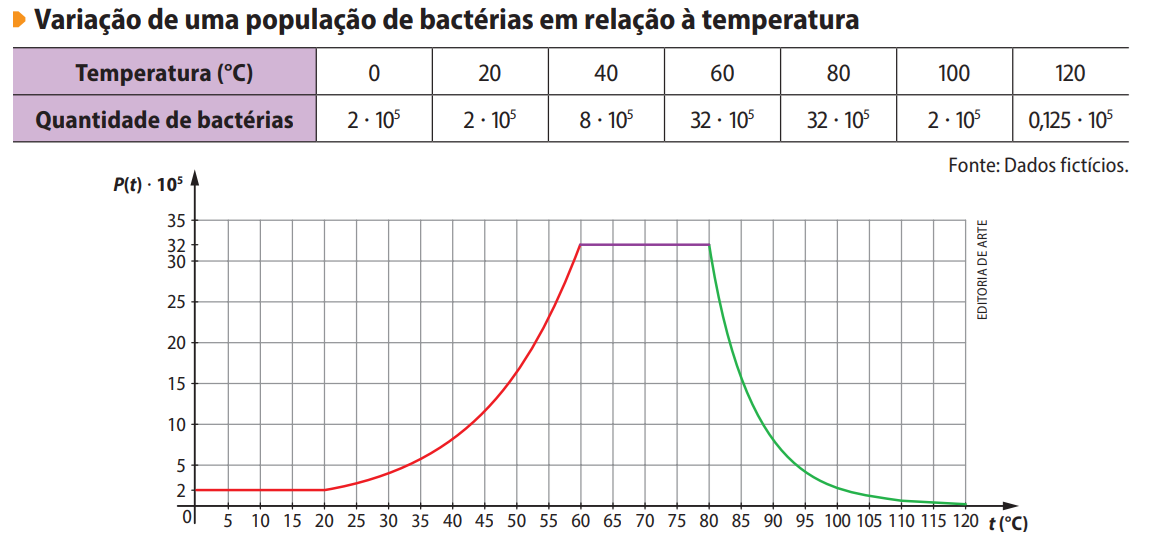
-
a) Para quais intervalos de temperatura a população de bactérias estudada aumentou, diminuiu ou se manteve estável?
b) Se o aumento da população de bactérias é dado por \( f(t) = 2^{0{,}1(t – 10)} \) e a diminuição, por \( g(t) = 32 – 2^{0{,}2(t – 80)} \), calcule a quantidade aproximada de bactérias nessa amostra, quando a temperatura atingiu:
- 30 °C
- 50 °C
- 90 °C
- 110 °C
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Vamos analisar o gráfico e usar as expressões fornecidas para o aumento e a diminuição da população bacteriana, conforme a temperatura aumenta.
a) Intervalos de variação:
- Estável de 0 °C a 20 °C (população constante em \( 2 \cdot 10^5 \))
- Aumento de 20 °C a 60 °C (crescimento exponencial)
- Estável de 60 °C a 80 °C (população constante em \( 32 \cdot 10^5 \))
- Diminuição de 80 °C a 120 °C (decrescimento exponencial)
b) Cálculo das quantidades:
- Para 30 °C: \[ f(30) = 2^{0{,}1(30 – 10)} = 2^2 = 4 \Rightarrow 4 \cdot 10^5 = \boxed{400\,000\ bactérias} \]
- Para 50 °C: \[ f(50) = 2^{0{,}1(50 – 10)} = 2^4 = 16 \Rightarrow 16 \cdot 10^5 = \boxed{1\,600\,000\ bactérias} \]
- Para 90 °C: \[ g(90) = 32 – 2^{0{,}2(90 – 80)} = 32 – 2^2 = 32 – 4 = 28\]\[ \Rightarrow 28 \cdot 10^5 = \boxed{800\,000\ bactérias} \]
- Para 110 °C: \[ g(110) = 32 – 2^{0{,}2(110 – 80)} = \]\[ 32 – 2^6 = 32 – 64 = -32 \]\[\ (\text{não faz sentido físico, usamos valor da tabela: }\]\[ 0{,}5 \cdot 10^5 = \boxed{50\,000\ bactérias}) \]
✅ Resumo final:
- a) Aumentou de 20 °C a 60 °C; estável de 0–20 °C e 60–80 °C; diminuiu de 80–120 °C
- b)
30 °C: 400 000 bactérias
50 °C: 1 600 000 bactérias
90 °C: 800 000 bactérias
110 °C: 50 000 bactérias (aproximado da tabela)
23. Para quais valores reais de \( k \), a função dada por \( f(x) = (k – 3)^x \) é decrescente?
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
A função exponencial \( f(x) = a^x \) é:
- Crescente se \( a > 1 \)
- Decrescente se \( 0 < a < 1 \)
- Indefinida para \( a \leq 0 \) em \( \mathbb{R} \)
Logo, queremos que a base \( a = k – 3 \) esteja no intervalo \( 0 < k - 3 < 1 \)
Etapa 1 – Montar a inequação:
Queremos: \[ 0 < k - 3 < 1 \]
Etapa 2 – Resolver a inequação composta:
Somando 3 em todos os membros: \[ 0 + 3 < k < 1 + 3 \Rightarrow 3 < k < 4 \]
✅ Conclusão:
Para que a função seja decrescente, o valor de \( k \) deve satisfazer: \[ \boxed{3 < k < 4} \]
🧠 Mapas Mentais de Matemática24. Copie o quadro a seguir, referente às funções definidas por \( f(x) = 3^x \), \( g(x) = 3^x + 2 \) e \( h(x) = 3^{x-2} \), e complete-o:
| Lei da função | x | -2 | -1 | 0 | 1 | 2 | 3 |
| \( f(x) = 3^x \) | |||||||
| \( g(x) = 3^x + 2 \) | |||||||
| \( h(x) = 3^{x – 2} \) |
Agora, faça o que se pede:
- Utilizando o GeoGebra, construa, em um mesmo sistema cartesiano, o gráfico de \( f \), de \( g \) e de \( h \).
- Ao analisar os gráficos construídos, podemos dizer que \( f \), \( g \) e \( h \) são funções crescentes ou decrescentes?
- Determine o domínio e o conjunto imagem dessas funções.
- Descreva como seria o gráfico da função dada por \( m(x) = 3^x – 2 \), em relação ao gráfico de \( f \), sem construí-lo.
- Descreva como seria o gráfico da função dada por \( q(x) = 3^{x + 2} \), em relação ao gráfico de \( f \), sem construí-lo.
- Construa, em um mesmo sistema cartesiano, os gráficos das funções \( f \), \( m \) e \( q \), e comprove as respostas dadas nos itens d e e.
🔍 Ver solução passo a passo
| Lei da função | x | -2 | -1 | 0 | 1 | 2 | 3 |
| \( f(x) = 3^x \) | \( \dfrac{1}{9} \) | \( \dfrac{1}{3} \) | 1 | 3 | 9 | 27 | |
| \( g(x) = 3^x + 2 \) | \( \dfrac{1}{9} + 2 \) | \( \dfrac{1}{3} + 2 \) | 1 + 2 | 3 + 2 | 9 + 2 | 27 + 2 | |
| \( h(x) = 3^{x – 2} \) | \( \dfrac{1}{81} \) | \( \dfrac{1}{27} \) | \( \dfrac{1}{9} \) | \( \dfrac{1}{3} \) | 1 | 3 |
a) A construção pode ser feita com o software GeoGebra, inserindo os comandos:
f(x) = 3^xg(x) = 3^x + 2h(x) = 3^(x - 2)
b) Todas as funções são exponenciais com base \( > 1 \).
✅ Resposta: As funções \( f \), \( g \) e \( h \) são crescentes.
c)
- Domínio: \( D(f) = D(g) = D(h) = \mathbb{R} \)
- Imagem:
\( \text{Im}(f) = \mathbb{R}_+^* \)
\( \text{Im}(g) = \{ y \in \mathbb{R} \mid y > 2 \} \)
\( \text{Im}(h) = \mathbb{R}_+^* \)
d) A função \( m(x) = 3^x – 2 \) é uma translação vertical para baixo do gráfico de \( f(x) = 3^x \).
Ou seja, cada ponto do gráfico de \( f \) é deslocado 2 unidades para baixo.
e) A função \( q(x) = 3^{x+2} \) representa uma translação horizontal para a esquerda do gráfico de \( f(x) = 3^x \), deslocando-o 2 unidades para a esquerda.
f) Ao construir os gráficos de \( f \), \( m \) e \( q \), podemos visualizar:
- \( m(x) \): gráfico mais abaixo, mesma forma que \( f \)
- \( q(x) \): gráfico deslocado para a esquerda
Esses deslocamentos confirmam as transformações descritas nos itens anteriores.
✅ Conclusão geral:
- \( f \), \( g \), \( h \), \( m \) e \( q \) são todas funções exponenciais crescentes
- Transformações em \( f \) afetam posição, mas não o crescimento
- Domínios continuam \( \mathbb{R} \), e as imagens variam conforme a translação vertical
25. Um banco possui taxa de rendimento na poupança de 0,35% ao mês. Um cliente que possui poupança nesse banco depositou R$ 1.000,00 no mês de janeiro e, ao longo de 6 meses, não realizou saques nem depositou quantia a mais. Conforme os dados da tabela, responda às questões:
| Mês | Poupança (R$) |
|---|---|
| Janeiro | 1.000,00 |
| Fevereiro | 1.000,00 × 1,0035 = 1.003,50 |
| Março | 1.003,50 × 1,0035 = 1.007,01 |
| Abril | 1.007,01 × 1,0035 = 1.010,53 |
| Maio | 1.010,53 × 1,0035 = 1.014,07 |
| Junho | 1.014,07 × 1,0035 = 1.017,62 |
-
a) Qual é a taxa de variação média aproximada da poupança entre o sexto e o primeiro mês desse ano?
b) Considerando que não houve saques nem depósitos nessa aplicação, determine a lei da função que representa o valor disponível em poupança em relação ao número de meses \( t \), em que o valor inicial foi aplicado.
c) Quanto esse cliente terá aproximadamente na poupança após 12 meses sem realizar saques ou depósitos?
🔍 Ver solução passo a passo
a) Taxa de variação média:
Valor final: R$ 1.017,62
Valor inicial: R$ 1.000,00
\[ \text{Variação média} = \frac{1.017,62 – 1.000,00}{6} = \frac{17,62}{6} ≈ \boxed{R\$ 3,52} \]
b) Lei da função:
Como se trata de juros compostos com taxa de 0,35% ao mês:
\[ f(t) = 1000 \cdot (1 + 0{,}0035)^t = \boxed{f(t) = 1000 \cdot (1{,}0035)^t} \]
c) Valor após 12 meses:
Aplicando \( t = 12 \) na função:
\[ f(12) = 1000 \cdot (1{,}0035)^{12} ≈ 1000 \cdot 1{,}04282 ≈ \boxed{R\$ 1.042,82} \]
✅ Conclusão:
- a) R$ 3,52 por mês (média)
- b) Função: \( f(t) = 1000 \cdot (1{,}0035)^t \)
- c) Após 12 meses: R$ 1.042,82