1. Introdução
Você sabia que entre 2020 e 2025, 7 questões de geometria espacial foram aplicadas na prova de Matemática da UNICAMP? Isso representa cerca de 7,28% do total das questões de matemática. Por isso, quem quer se destacar precisa dominar esse conteúdo com profundidade. Este artigo explora tudo que você precisa saber sobre geometria espacial Unicamp vestibular, com insights, metodologia, dicas de estudo e espaço organizado para inserir as suas 7 questões.
2. Panorama Estatístico e Relevância
- Total de questões de geometria espacial (2020–2025): 7
- Percentual aproximado: 7,28% das questões de matemática
- Importância: apesar de ser menor que geometria plana, a frequência é significativa e ocorre com consistência na prova discursiva da UNICAMP.
Esses dados indicam que a banca COMVEST valoriza não apenas os temas clássicos, mas também a habilidade de lidar com sólidos, volumes e áreas espaciais.
3. Conteúdos mais frequentes em geometria espacial no vestibular da UNICAMP
As questões costumam explorar:
- Cálculo de volume e área de superfícies — prismas, pirâmides, cilindros, cones, esferas e troncos.
- Relações métricas em sólidos — teoremas de Cavalieri, consolidação de seções transversais, semelhança espacial.
- Problemas envolvendo deslocamento de líquidos, densidade ou empacotamentos.
- Geometria espacial combinada com análise de simetria, posição ou interseções de planos.
- Visualização tridimensional — interpretação de cortes, pontos médios espaciais, projeções e seções planas.
Você verá como esses temas aparecem sistematicamente nas questões concretas da banca.
4. Metodologia de Resolução Ideal
4.1. Compreensão da figura tridimensional
- Identifique o sólido envolvido (prisma, pirâmide, cilindro, entre outros).
- Marque arestas, bases, e identifique se há cortes, seções ou movimentos rotacionais da figura.
Matemática UNICAMP: Guia Completo do Vestibular com Questões Resolvidas
4.2. Desenho auxiliar e projeções
- Faça cortes que transformem o sólido em partes conhecidas (por exemplo, pirâmide mais prisma).
- Use projeção em planta para visualizar a base e a altura adequadamente.
4.3. Aplicação de fórmulas e teoremas
📘 Fórmulas de Geometria Espacial
📦 Prisma e Cubo
Volume do Prisma: $$ V = A_{base} \cdot h $$
Volume do Cubo: $$ V = a^3 $$
Área Total do Cubo: $$ A_{total} = 6a^2 $$
🔺 Pirâmide
Volume: $$ V = \frac{1}{3} \cdot A_{base} \cdot h $$
🟦 Cilindro
Volume: $$ V = \pi \cdot r^2 \cdot h $$
Área Lateral: $$ A_{lateral} = 2 \cdot \pi \cdot r \cdot h $$
Área Total: $$ A_{total} = 2 \cdot \pi \cdot r \cdot (r + h) $$
🛎️ Cone
Volume: $$ V = \frac{1}{3} \cdot \pi \cdot r^2 \cdot h $$
Área Lateral: $$ A_{lateral} = \pi \cdot r \cdot g $$
Área Total: $$ A_{total} = \pi \cdot r \cdot (r + g) $$
(onde \( g \) é a geratriz)
🌐 Esfera
Volume: $$ V = \frac{4}{3} \cdot \pi \cdot r^3 $$
Área Total: $$ A = 4 \cdot \pi \cdot r^2 $$
✅ Estude com atenção cada fórmula e pratique exercícios da UNICAMP envolvendo sólidos simples e compostos.
4.4. Ética no cômputo e verificação
- Verifique se as unidades estão corretas.
- A consistência visual deve ser coerente: volume menor que o sólido inteiro, e área total condizente com o esperado.
- Em casos de sobreposição ou volume de líquido, use diferença entre volumes ou regra de três com densidade.
Geometria Plana Unicamp Vestibular: O Guia Definitivo (2020–2025)
5. Questões Comentadas
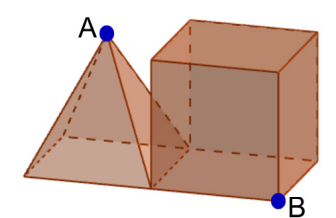
A figura abaixo mostra uma pirâmide e um cubo, que compartilham uma aresta da base da pirâmide. A pirâmide tem altura de 1 m e base quadrada de 1 m de lado. O cubo também possui arestas de 1 m.
a) Um sólido é formado pela união desses dois objetos. Qual é o seu volume?
b) Determine a distância do ponto A (vértice superior da pirâmide) até o ponto B (vértice frontal da base do cubo que não está na aresta em comum com a pirâmide).
a) Volume do sólido
O volume do sólido é a soma do volume do cubo com o da pirâmide: \[ V = 1^3 + \frac{1}{3} \cdot 1^2 \cdot 1 = \frac{4}{3} \text{ m}^3 \]
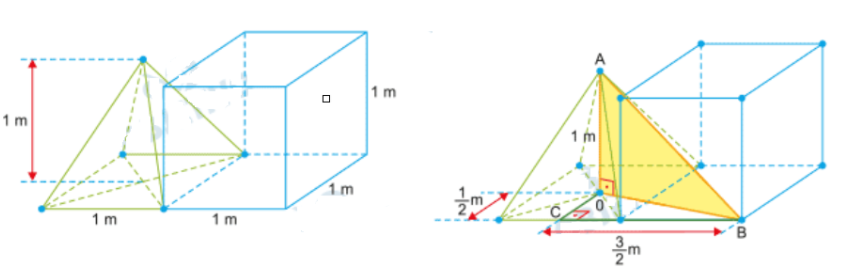
b) Distância de A até B
Considerando a projeção ortogonal:
- No triângulo retângulo \( CBO \): \[ OB^2 = \left(\frac{1}{2}\right)^2 + \left(\frac{3}{2}\right)^2 = \frac{10}{4} \]
- No triângulo retângulo \( OBA \): \[ AB^2 = AO^2 + OB^2 = 1^2 + \frac{10}{4} = \frac{14}{4} \]
Logo: \[ AB = \frac{\sqrt{14}}{2} \text{ m} \]
Resposta Final: a) \( \frac{4}{3} \, \text{m}^3 \) b) \( \frac{\sqrt{14}}{2} \, \text{m} \)
Márcia está decorando sua casa para o Natal e pretende cobrir uma pilastra com papel de parede de temas natalinos e depois enrolar uma fita de lâmpadas de led na pilastra coberta, dando uma única volta, de modo que o ponto em que a fita começa a ser enrolada esteja exatamente embaixo do ponto onde ela termina, como ilustrado na figura a seguir.
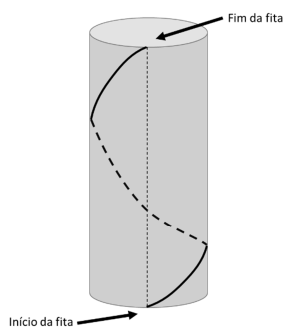
A pilastra tem o formato de um cilindro circular reto com 3 m de altura; a medida do perímetro da circunferência da base é 1 m, e sua lateral será coberta completamente com papel de parede colado sem sobreposição.
a) Sabendo que o metro quadrado do papel de parede custa R$ 20,00,
determine quanto Márcia terá que gastar em papel de parede para cobrir a pilastra.
b) Qual é o menor comprimento que a fita de led precisa ter para ser possível essa instalação?
a) Cálculo do custo com papel de parede:
A área lateral do cilindro é dada por: \[ A = \text{perímetro da base} \times \text{altura} = 1 \times 3 = 3 \text{ m}^2 \]
O custo total será: \[ 3 \times R\$20,00 = R\$60,00 \]
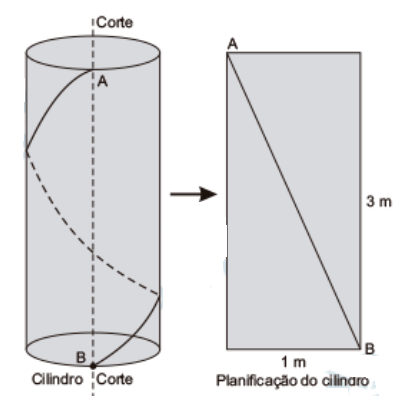
b) Comprimento mínimo da fita de led:
Ao planificar o cilindro, obtemos um retângulo de 3 m de altura e 1 m de base. A fita de led corresponde à diagonal desse retângulo: \[ d = \sqrt{1^2 + 3^2} = \sqrt{10}\text{ m} \]
Resposta final:
- a) R$ 60,00
- b) \(\sqrt{10}\) m
Um recipiente cilíndrico de altura \(h\) tem água em seu interior. Ao mergulhar uma esfera de chumbo de raio \(R\) neste recipiente, a água cobre a esfera e nenhuma quantidade de água se perde, como ilustrado na figura a seguir.
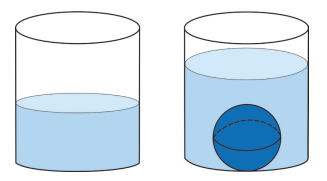
Sabendo que o raio da base do cilindro é o dobro do raio da esfera, a diferença entre a altura da água antes e depois do mergulho da esfera é igual a:
-
a) 2R
b) R
c) R/3
d) 2R/3
1) Relação entre volumes:
O volume da esfera de raio \(R\) é: \[ V_{\text{esfera}} = \frac{4}{3}\pi R^3 \]
O volume do cilindro que corresponde à variação de altura \(h\) da água tem raio \(2R\) e altura \(h\): \[ V_{\text{cilindro}} = \pi (2R)^2 \cdot h = 4\pi R^2 h \]
2) Igualando os volumes deslocados:
\[ \frac{4}{3}\pi R^3 = 4 \pi R^2 \cdot h \]
Simplificando: \[ \frac{R}{3} = h \]
3) Conclusão:
A diferença na altura da água é R/3. Resposta: C.
a) 17 de março. b) 18 de março. c) 19 de março. d) 20 de março.
- Cálculo do volume utilizado no 1º dia (16/03):
O cilindro tem raio \( r = 3 \text{ cm} \) e altura utilizada \( h = 5 \text{ cm} \). \[ V = \pi r^2 h \approx 3 \cdot 3^2 \cdot 5 = 135 \text{ cm}^3 \] - Quantidade de dias até acabar o frasco: \[ \frac{500}{135} \approx 3{,}7 \] Ou seja, o álcool dura 3 dias completos e termina no 4º dia.
- Considerando 16/03 como o 1º dia, o álcool acabará em **19/03**.
- Portanto, a resposta correta é **C**.
UNICAMP 2022 | Matemática | Geometria Espacial e Custos
Um fabricante de produtos de beleza está modificando as dimensões da embalagem de seu principal produto, o shampoo antipiolhos chamado 100𝜋olho. Atualmente, as embalagens têm o formato de um paralelepípedo com 18 cm de altura e com base retangular de dimensões 2 cm × 3 cm.
São utilizados dois tipos de materiais para construir a embalagem. O material utilizado tanto para a base quanto para a lateral é mais simples e custa R$ 10,00 o metro quadrado. O material utilizado para a tampa custa R$ 40,00 o metro quadrado, por ser mais resistente. a) Qual o custo atual do material para construir 100 embalagens? b) Por questões logísticas, as novas embalagens devem ter o formato de um paralelepípedo com base quadrada e com altura de 12 cm, e precisam ter a mesma capacidade volumétrica que as embalagens atuais. Quais as dimensões da nova embalagem e o custo de produção de 100 delas, considerando os mesmos materiais para produção?Resolução:
1) Volume da embalagem atual:
\[ V = 2 \times 3 \times 18 = 108\,\text{cm}^3 \]2) Área da base + lateral:
\[ A_\text{base+lateral} = 3 \times 2 + 2 \times (3+2)\times18 = 186\,\text{cm}^2 \] Convertendo para metros quadrados: \[ 0,0186\, m^2 \]3) Área da tampa:
\[ 3 \times 2 = 6\,\text{cm}^2 = 0,0006\, m^2 \]4) Custo de 100 embalagens atuais:
\[ 100 \times (0,0186 \times 10 + 0,0006 \times 40) = 21\,\text{reais} \]5) Nova embalagem: base quadrada de lado \(x\) e altura 12 cm.
\[ x^2 \cdot 12 = 108 \quad\Rightarrow\quad x = 3\,\text{cm} \]6) Área da base + lateral:
\[ 3^2 + 4\cdot 3\cdot 12 = 153\,\text{cm}^2 = 0,0153\,m^2 \]7) Área da tampa:
\[ 3^2 = 9\,\text{cm}^2 = 0,0009\, m^2 \]8) Custo de 100 novas embalagens:
\[ 100 \times (0,0153 \times 10 + 0,0009 \times 40) = 18,90\,\text{reais} \] a) R\$ 21,00b) Lado = 3 cm e custo R\$ 18,90
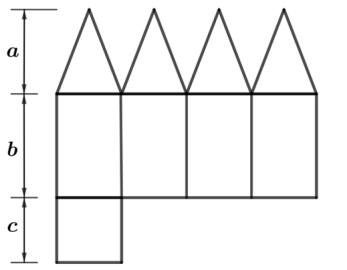
a) Determine o número de vértices e de arestas desse poliedro.
b) Para \(a = 13 \text{ cm}\), \(b = 16 \text{ cm}\) e \(c = 10 \text{ cm}\), calcule o volume desse poliedro.
- Identificação do poliedro:
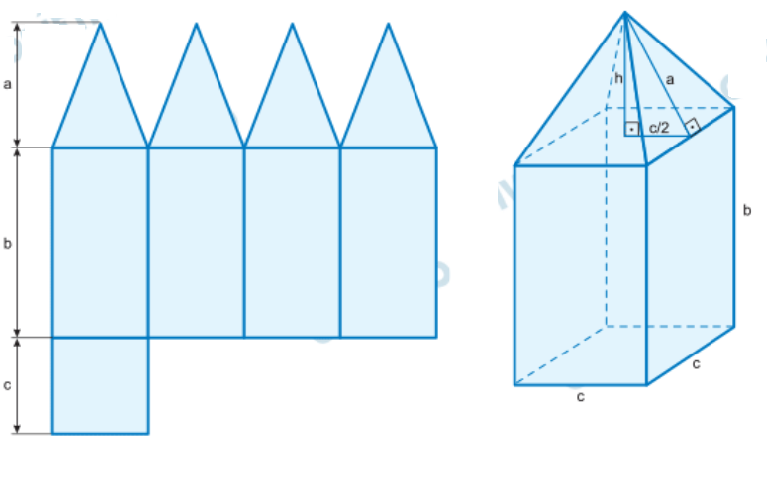
O poliedro é formado por uma pirâmide reta sobre um paralelepípedo reto-retângulo.
– Base da pirâmide: quadrado de lado \(c\) – Altura da face lateral da pirâmide: \(a\) – Base do paralelepípedo: quadrado de lado \(c\) – Altura do paralelepípedo: \(b\)
Logo, o poliedro possui **9 vértices e 16 arestas**.- Cálculo do volume:
Primeiro, calculamos a altura \(h\) da pirâmide usando Pitágoras: \[ a^2 = h^2 + \left(\frac{c}{2}\right)^2 \quad \Rightarrow \quad 13^2 = h^2 + 5^2 \quad \Rightarrow \quad h = 12 \text{ cm} \] O volume do poliedro é a soma do volume da pirâmide e do paralelepípedo: \[ V = \frac{1}{3} c^2 h + c^2 b \] \[ V = \frac{1}{3} \cdot 10^2 \cdot 12 + 10^2 \cdot 16 = 2000 \text{ cm}^3 \]Respostas:
- a) 9 vértices e 16 arestas
- b) \(2000 \text{ cm}^3\)
- Cálculo do volume:
- Equacionando as áreas de superfície:
– Área do tetraedro regular: \( 4 \cdot \frac{\ell^2 \sqrt{3}}{4} = \ell^2 \sqrt{3} \) – Área do cubo: \( 6a^2 \) - Igualando as áreas: \[ \ell^2 \sqrt{3} = 6 a^2 \] \[ \frac{\ell^2}{a^2} = \frac{6}{\sqrt{3}} = 2 \sqrt{3} \] \[ \frac{\ell}{a} = \sqrt{2\sqrt{3}} = \sqrt{2} \cdot \sqrt[4]{3} \]
- Razão final: \[ \frac{\ell}{a} = \sqrt{2} \cdot \sqrt{3} \]
Resposta correta: c) \( \sqrt{2} \cdot \sqrt{3} \)
6. Dicas Estratégicas de Estudo
- Resolva profundamente as 7 questões de geometria espacial da UNICAMP entre 2020 e 2025, compreendendo cada detalhe.
- Estude exercícios de cilindros, cones, pirâmides, esferas, prismas e troncos, especialmente os que envolvem cálculo de volumes e áreas combinadas.
- Pratique visualização espacial: desenhe sólidos, marque cortes e compreenda diferentes posições relativas.
- Utilize o Geogebra ou aplicativos CAD para modelar sólidos e entender comportamento de cortes e volumes.
- Cronometre a resolução para melhorar velocidade sem perder a precisão.
- Relacione geometria espacial a outros conteúdos da prova: porcentagem, equações, geometria analítica, trigonometria espacial.
7. Exemplos de Aplicações Típicas
- Determinar volume de um sólido composto (por exemplo, cilindro com topo em forma de tronco).
- Calcular altura ou raio a partir da igualdade entre volume e área ou densidade/deposição de líquido.
- Aplicar semelhança espacial para encontrar razões de volume entre sólidos análogos.
- Lidar com seções planas em pirâmides e prismas, visualizando cortes que simplificam o cálculo.
📘 Questões MATEMÁTICA UNICAMP Resolvidas
Escolha o ano e acesse as questões com solução passo a passo:
8. Conclusão
Dominar geometria espacial Unicamp vestibular é crucial: apesar de representar cerca de 7 questões entre 2020 e 2025, o tema cobra raciocínio tridimensional, precisão e visão integrada. Este guia fornece a base textual e estratégica para você inserir as suas perguntas manualmente, resolver com método e garantir que todas as etapas estejam organizadas: enunciado, figura, resolução lógica e insight de aprendizagem.
Estude com constância, visualize os sólidos e treine as sete questões reais com cuidado — e você estará pronto para encarar qualquer questão de geometria espacial na UNICAMP com confiança 💡.






















