📈 Gráficos da Função Exponencial
Vamos agora representar graficamente funções do tipo exponencial, ou seja, funções da forma:
$$ f(x) = a^x $$
🔺 Exemplo 1 – Função Crescente: \( f(x) = 2^x \)
Veja a tabela de valores:
| x | \( f(x) = 2^x \) |
|---|---|
| -3 | 1/8 |
| -2 | 1/4 |
| -1 | 1/2 |
| 0 | 1 |
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
Gráfico de \( f(x) = 2^x \)
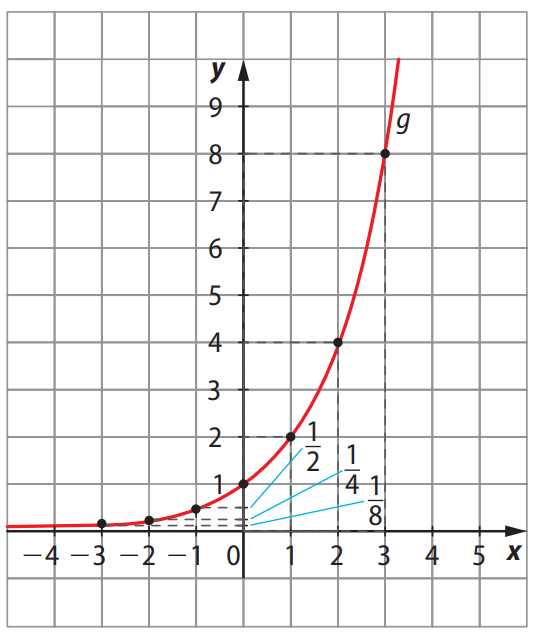
🔻 Exemplo 2 – Função Decrescente: \( f(x) = \left(\frac{1}{2}\right)^x \)
Veja a tabela de valores:
| x | \( f(x) = \left(\frac{1}{2}\right)^x \) |
|---|---|
| -3 | 8 |
| -2 | 4 |
| -1 | 2 |
| 0 | 1 |
| 1 | 1/2 |
| 2 | 1/4 |
| 3 | 1/8 |
Gráfico de \( f(x) = \left(\frac{1}{2}\right)^x \)
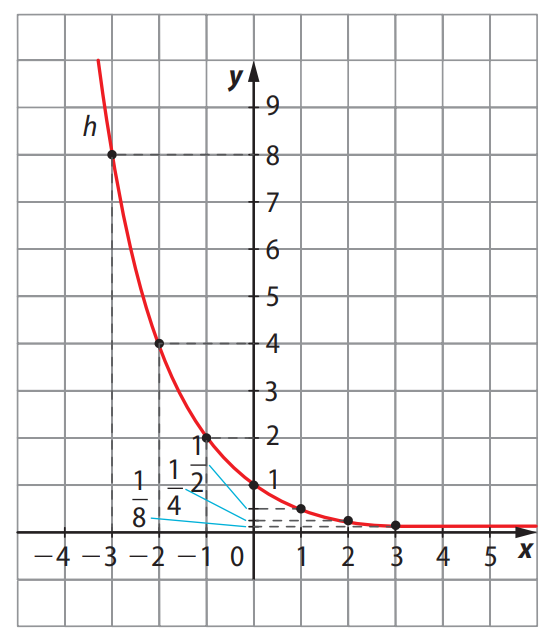
🧠 Propriedades Gerais da Função Exponencial \( f(x) = a^x \)
- Domínio: \( \mathbb{R} \)
- Imagem: \( \mathbb{R}^+ \)
- Ponto comum dos gráficos: Todas as funções passam por \( (0, 1) \)
- Assíntota horizontal: Eixo x (a função nunca toca o eixo)
Podemos dizer que os gráficos de \( f(x) = 2^x \) e \( f(x) = \left(\frac{1}{2}\right)^x \) são simétricos em relação ao eixo y?
📈 Exercícios Resolvidos – Gráfico da Função Exponencial
Ver solução
\( f(2) = 3^2 = 9 \)
Como \( a = 3 > 1 \), o gráfico é crescente.
Resposta: \( f(2) = 9 \), gráfico crescente.
Ver solução
\( g(2) = \left(\frac{1}{3}\right)^2 = \frac{1}{9} \)
Como a base está entre 0 e 1, o gráfico é decrescente.
Resposta: \( g(2) = \frac{1}{9} \), gráfico decrescente.
Ver solução
Se \( x = 0 \), então \( f(0) = a^0 = 1 \), qualquer que seja a base válida.
Resposta: O ponto \( (0, 1) \) sempre pertence ao gráfico.
Ver solução
\( g(x) = \left(\frac{1}{2}\right)^x = 2^{-x} \)
Ou seja, é o reflexo do gráfico de \( f(x) = 2^x \) em relação ao eixo y.
Resposta: São simétricos em relação ao eixo y.
Ver solução
Não. Toda função exponencial com \( a > 0 \) e \( a \ne 1 \) tem assíntota horizontal no eixo x.
Resposta: Não cruza o eixo x. O eixo x é uma assíntota horizontal.






















