Hexágono Regular: Propriedades, Fórmulas e Aplicações

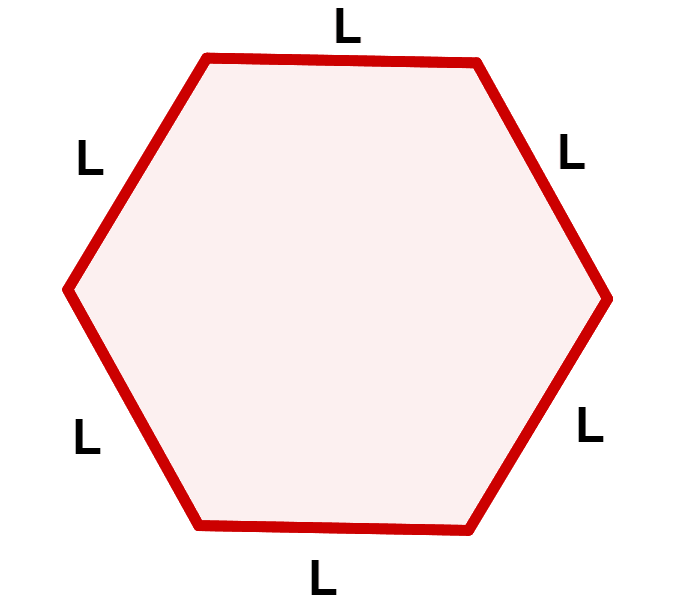
Um hexágono é um polígono de seis lados e, quando todos os seus lados e ângulos internos são iguais, ele é classificado como um hexágono regular. Este tipo de hexágono possui propriedades e características únicas, que o tornam especialmente interessante na geometria. Neste artigo, vamos explorar essas propriedades, fórmulas para calcular perímetro e área, além de algumas aplicações práticas.

Características do Hexágono Regular

1. Lados Iguais: Todos os seis lados de um hexágono regular possuem a mesma medida.
2. Ângulos Internos Iguais: Todos os ângulos internos de um hexágono regular são iguais a 120 graus.
3. Simetria: O hexágono regular possui simetria rotacional de ordem 6 e 6 eixos de simetria reflexiva.
4. Círculo Circunscrito e Inscrito: Um hexágono regular pode ser inscrito em um círculo, e também possui um círculo inscrito, tocando todos os seus lados.

Fórmulas Importantes

1. Perímetro do Hexágono Regular:

O perímetro (P) de um hexágono regular é a soma de todos os seus lados. Como todos os lados têm o mesmo comprimento (l), o perímetro é dado por:

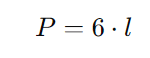
2. Área do Hexágono Regular:

A área (A) de um hexágono regular pode ser calculada utilizando a fórmula:

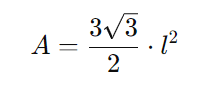
onde:

• (l) é o comprimento de um lado do hexágono.

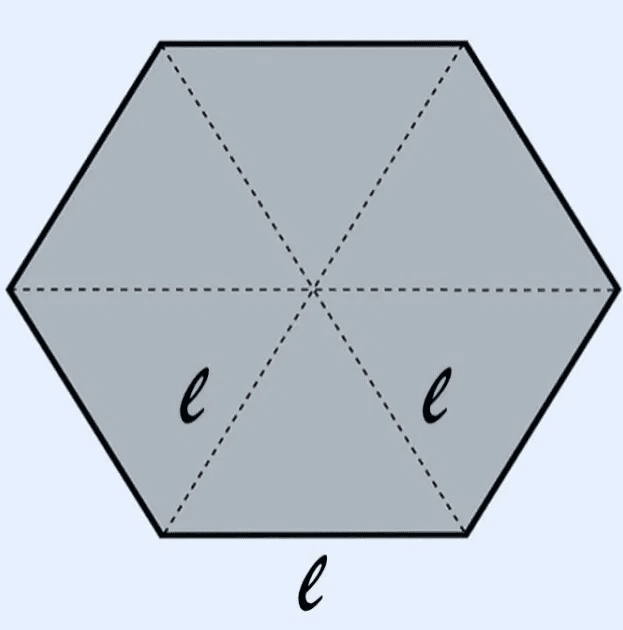
Outra forma de calcular a área é dividir o hexágono em 6 triângulos equiláteros e calcular a área de cada um deles. A área de um triângulo equilátero é dada por:

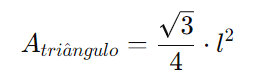
Como há 6 triângulos equiláteros, a área total do hexágono é:

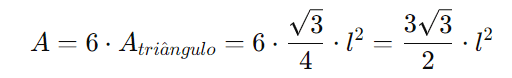
Propriedades Geométricas do Hexágono Regular

1. Ângulos Internos: Como mencionado, cada ângulo interno de um hexágono regular é de 120 graus. A soma dos ângulos internos de qualquer polígono é dada por:

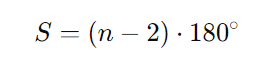
onde (n) é o número de lados. Para o hexágono ((n = 6)):

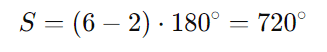
Como os ângulos internos são iguais, cada um é:

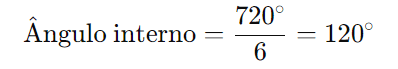
2. Apótema: O apótema de um hexágono regular é a distância do centro até o meio de um dos lados. O apótema (a) pode ser calculado como:

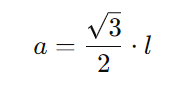
Aplicações Práticas do Hexágono Regular

Os hexágonos regulares aparecem frequentemente em contextos naturais e artificiais. Algumas aplicações incluem:

1. Favos de Mel: A estrutura dos favos de mel nas colmeias é formada por hexágonos regulares, o que maximiza a eficiência do espaço e minimiza o uso de cera para criar compartimentos de armazenamento.
2. Design e Arquitetura: Hexágonos regulares são usados em pavimentação, azulejos e outros elementos de design devido à sua simetria e capacidade de cobrir superfícies planas sem lacunas.
3. Mecânica e Engenharia: Estruturas hexagonais são usadas em materiais compostos para aumentar a resistência e reduzir o peso.

Exemplo de Cálculo

Suponha que desejamos calcular o perímetro e a área de um hexágono regular cujo lado mede 5 cm.

• Perímetro:

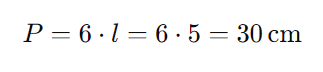
• Área:

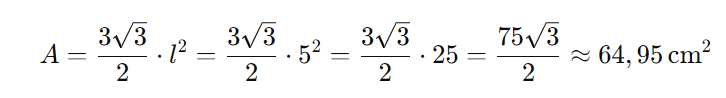
Conclusão

O hexágono regular é um polígono fascinante com inúmeras propriedades e aplicações. Suas características geométricas, como lados e ângulos iguais, e a presença de simetria, o tornam uma figura essencial no estudo da geometria. Com fórmulas simples, é possível calcular o perímetro e a área, facilitando sua aplicação em diversos contextos do mundo real.

A geometria é uma área fundamental da matemática, dedicada ao estudo das formas, tamanhos e propriedades de figuras no plano e no espaço.

Exercício Hexágono Regular

Uma empresa de hotelaria irá construir bangalôs em forma de hexágonos regulares com lados de tamanho igual a 4 metros. Desse modo, a área de cada um desses bangalôs será de

A) 6√3 m².

B) 8√3 m².

C) 96√3 m².

D) 24√3 m².

E) 48√3 m².

Solução em Vídeo

Para calcular a área de um hexágono regular, usamos a fórmula:

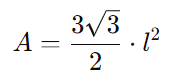
onde (l) é o comprimento do lado do hexágono.

Passo a Passo:

1. Identifique o valor do lado do hexágono: O lado do hexágono regular é dado por (l = 4) metros.
2. Substitua o valor na fórmula da área:

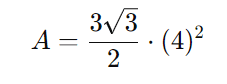
1. Calcule o quadrado de 4:

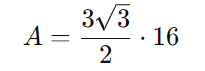
1. Multiplique e simplifique:

Conclusão:

A área de cada bangalô é 24√3 m².

Portanto, a resposta correta é:

D) 24√3 m².