Imagem de uma Função
Definição, diferenças para contradomínio, exemplos visuais e exercícios resolvidos.
Na teoria de conjuntos numéricos e funções, a imagem é o conjunto de todos os valores que a função realmente assume. É um conceito-chave para identificar se a função é injetora, sujeitora (sobrejetora) e para resolver problemas de ENEM e concursos.
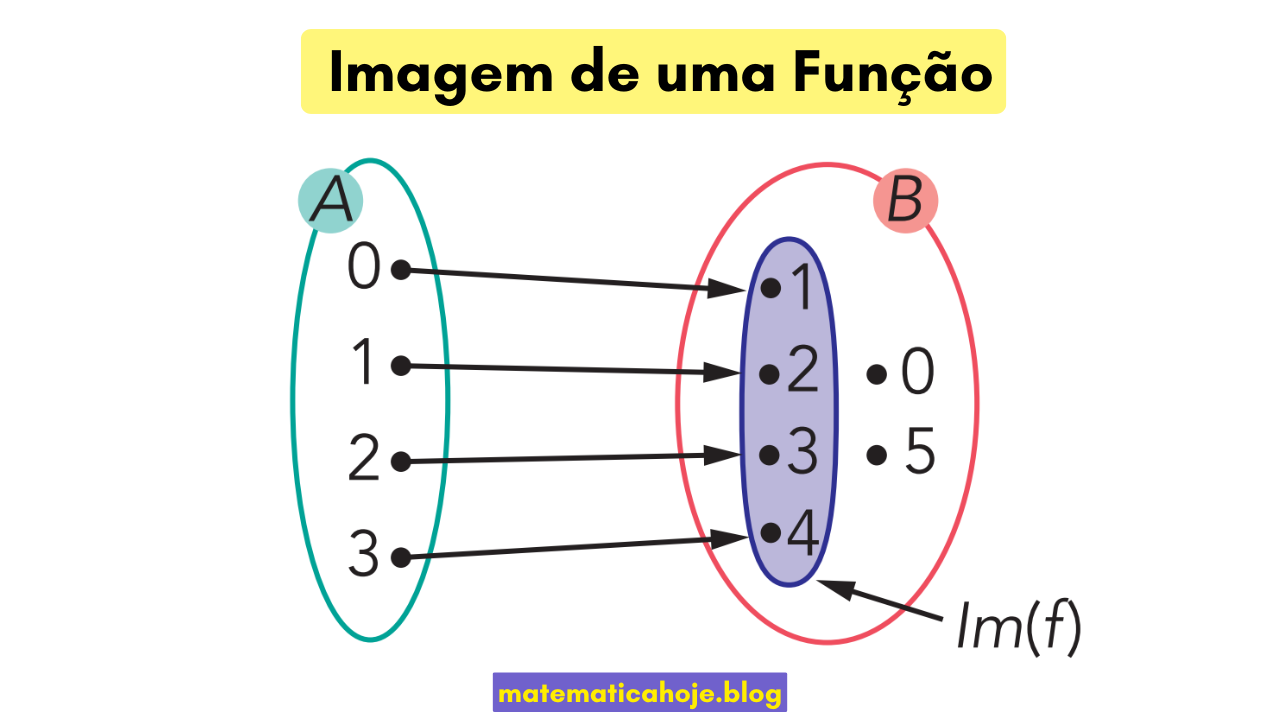
Imagem × Contradomínio
O contradomínio \(B\) é escolhido quando definimos \(f\). A imagem é o subconjunto de \(B\) efetivamente atingido pela função.
Se \(\mathrm{Im}(f)=B\), a função é sobrejetora.
Leituras relacionadas
Domínio de uma Função • Equações do 1º Grau • Logaritmos • Operações com Frações
Exemplos comentados
Exemplo 1 — Diagrama da figura
Considere \(A=\{0,1,2,3\}\) e \(B=\{0,1,2,3,4,5\}\) com \(f(x)=x+1\).
| \(x\in A\) | \(f(x)\) |
|---|---|
| 0 | 1 |
| 1 | 2 |
| 2 | 3 |
| 3 | 4 |
Imagem: \(\{1,2,3,4\}\) (subconjunto de \(B\)).
Exemplo 2 — Função afim
Se \(g:\mathbb{R}\to\mathbb{R}\) com \(g(x)=2x-3\), então \(\mathrm{Im}(g)=\mathbb{R}\) (qualquer real é obtido resolvendo \(y=2x-3\Rightarrow x=\tfrac{y+3}{2}\)).
Exemplo 3 — Quadrática
\(h(x)=x^2+1=(x-0)^2+1\). Mínimo \(=1\) em \(x=0\). Logo, \(\mathrm{Im}(h)=[1,\infty)\).
Exemplo 4 — Racional
\(p(x)=\dfrac{1}{x-2}\). Não existe \(p(x)=0\). A imagem é \(\mathbb{R}\setminus\{0\}\).
Exemplo 5 — Logarítmica
\(q(x)=\ln x\) com domínio \((0,\infty)\). Sua imagem é \((-\infty,\infty)\).
Resolver mais questões sobre imagem de funçõesExercícios (múltipla escolha) com solução
1) Para \(f:A\to B\) com \(A=\{0,1,2,3\}\) e \(f(x)=x+1\), qual é \(\mathrm{Im}(f)\)?
- \(\{0,1,2,3\}\)
- \(\{1,2,3,4\}\)
- \(\{2,3,4,5\}\)
- \(\{0,2,3,4\}\)
Ver solução
2) Seja \(g:\mathbb{R}\to\mathbb{R}\) dada por \(g(x)=x^2-4x+5\). Determine \(\mathrm{Im}(g)\).
- \((-\infty,\infty)\)
- \([1,\infty)\)
- \([5,\infty)\)
- \((-\infty,1]\)
Ver solução
3) Para \(p(x)=\dfrac{1}{x-3}\) definida em \(\mathbb{R}\setminus\{3\}\), a imagem é:
- \(\mathbb{R}\)
- \(\mathbb{R}\setminus\{0\}\)
- \((0,\infty)\)
- \((-\infty,0)\)
Ver solução
4) Para \(q(x)=\ln(x-1)\), com domínio \(x>1\), qual é a imagem?
- \((-\infty,\infty)\)
- \((0,\infty)\)
- \([0,\infty)\)
- \((-\infty,0)\)
Ver solução
5) Para \(r(x)=\sqrt{4-x^2}\), a imagem é:
- \([0,2]\)
- \((-\infty,\infty)\)
- \([0,\infty)\)
- \((-2,2)\)
Ver solução
6) Considere \(s(x)=|x-2|\). Qual é \(\mathrm{Im}(s)\)?
- \((-\infty,\infty)\)
- \([0,\infty)\)
- \((0,\infty)\)
- \([2,\infty)\)
Ver solução
Continue estudando
- Mapas Mentais de Matemática
- Coleção 10 eBooks de Matemática
- Banco de Questões Matemática
- Função do 2º Grau






















