Lei dos Cossenos
A Lei dos Cossenos é um teorema fundamental da trigonometria que permite calcular lados ou ângulos de um triângulo qualquer, mesmo quando não se trata de um triângulo retângulo. É considerada uma generalização do Teorema de Pitágoras.
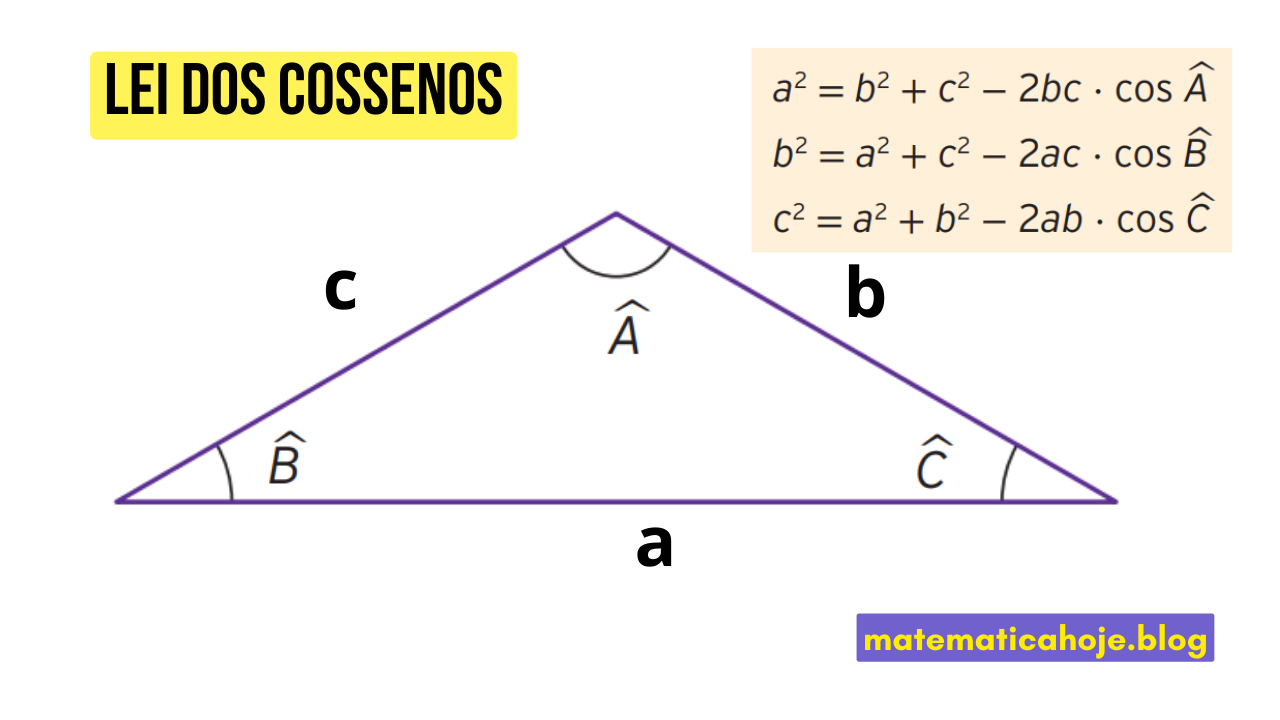
Fórmulas da Lei dos Cossenos
Onde:
- \(a, b, c\) são os lados do triângulo.
- \(\hat{A}, \hat{B}, \hat{C}\) são os ângulos opostos a cada lado.
Relação com o Teorema de Pitágoras
Se o triângulo for retângulo (\(\hat{A} = 90^\circ\)), temos que \(\cos \hat{A} = 0\). Nesse caso, a fórmula da Lei dos Cossenos se reduz a:
Ou seja, o próprio Teorema de Pitágoras.
Exemplo resolvido
Exemplo: Num triângulo, sabemos que \(a = 8\), \(b = 6\) e \(\hat{C} = 60^\circ\). Determine o lado \(c\).
Solução:
Pela Lei dos Cossenos:
\(c^2 = a^2 + b^2 – 2ab \cdot \cos \hat{C}\)
\(c^2 = 8^2 + 6^2 – 2 \cdot 8 \cdot 6 \cdot \cos 60^\circ\)
\(c^2 = 64 + 36 – 96 \cdot 0,5 = 100 – 48 = 52\)
\(c = \sqrt{52} \approx 7,21\).
Exercícios de prática
1) Num triângulo, temos \(a = 7\), \(b = 9\) e \(\hat{C} = 120^\circ\). Determine o valor de \(c\).
- 10
- 11
- 13
- 15
Ver solução
\(c^2 = 7^2 + 9^2 – 2 \cdot 7 \cdot 9 \cdot \cos 120^\circ\)
\(c^2 = 49 + 81 – 126 \cdot (-0,5)\)
\(c^2 = 130 + 63 = 193\)
\(c \approx 13,9 \approx 13\).
2) Num triângulo, \(b = 5\), \(c = 8\) e \(a = 10\). Determine o ângulo \(\hat{A}\).
- 45°
- 60°
- 75°
- 90°
Ver solução
Pela Lei dos Cossenos:
\(\cos \hat{A} = \dfrac{b^2 + c^2 – a^2}{2bc}\)
\(\cos \hat{A} = \dfrac{25 + 64 – 100}{2 \cdot 5 \cdot 8} = \dfrac{-11}{80} \approx -0,137\)
\(\hat{A} \approx 97,9^\circ \approx 98^\circ\).






















