Lei dos Cossenos
A Lei dos Cossenos generaliza Pitágoras para qualquer triângulo \(ABC\). Relaciona um lado ao ângulo compreendido entre os outros dois e é ideal para os casos SAS (dois lados + ângulo entre eles) e SSS (três lados).
Fórmula (equações cíclicas)
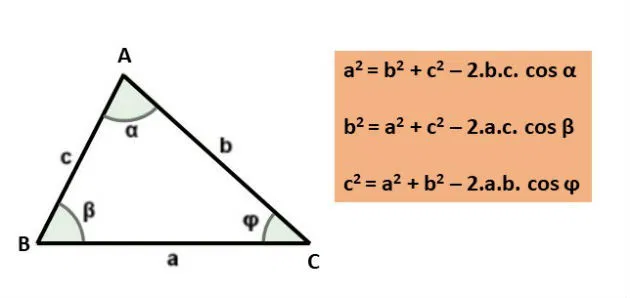
Quando usar
SAS: dois lados conhecidos e o ângulo compreendido ⇒ encontra-se o terceiro lado.
SSS: três lados conhecidos ⇒ calcula-se um ângulo isolando o cosseno.
Para dois lados e um ângulo não compreendido (SSA), prefira a Lei dos Senos.
Exemplos resolvidos (situação-problema)
Exemplo 1 — Encontrar um lado (SAS)
Cenário: em um palco, duas rampas metálicas com comprimentos \(b=7\) m e \(c=10\) m são montadas formando um ângulo de \(\alpha=30^\circ\) entre elas (ângulo compreendido). Pergunta: qual deve ser o comprimento da travessa que fecha o triângulo, oposta a esse ângulo? (lado \(a\)).
Ver solução
Exemplo 2 — Encontrar um ângulo (SSS)
Oficina de marcenaria: uma peça triangular deve encaixar em um nicho, com lados medidos \(a=8\) cm, \(b=5\) cm e \(c=7\) cm. Pergunta: qual é o ângulo de abertura no vértice oposto a \(a\) (isto é, \(\alpha\)) para regular a serra?
Ver solução
Exemplo 3 — Verificação de esquadro (classificação do ângulo)
Montagem de quadro: barras com \(b=9\) cm e \(c=12\) cm formam um triângulo cujo lado oposto mede \(a=15\) cm. Pergunta: o ângulo \(\alpha\) oposto a \(a\) é agudo, reto ou obtuso? Use a Lei dos Cossenos para confirmar o esquadro.
Ver solução
Exemplo 4 — Distância por triangulação (SAS)
Topografia de campo: a partir do ponto \(B\), mede-se a distância até \(A\) (\(b=350\) m) e até \(C\) (\(c=280\) m). O ângulo de visada entre as direções \(BA\) e \(BC\) é \(\alpha=112^\circ\) (obtuso), isto é, o ângulo compreendido. Pergunta: qual é a distância direta entre \(B\) e \(C\) (lado \(a\))?
Ver solução
Observações úteis
Redução a Pitágoras: se \(\alpha=90^\circ\), então \(\cos\alpha=0\) e \(a^{2}=b^{2}+c^{2}\).
Ângulo obtuso: \(\cos\alpha<0\) ⇒ \(a^2>b^2+c^2\) (o lado oposto é o maior).
Abordagem vetorial: o produto escalar \( \mathbf{u}\!\cdot\!\mathbf{v}=||\mathbf{u}||\,||\mathbf{v}||\cos\theta \) oferece outra demonstração elegante.
Exercícios propostos
1) \(b=9\), \(c=11\), \(\alpha=47^\circ\). Calcule \(a\).
2) \(a=10\), \(b=13\), \(c=15\). Encontre \(\gamma\).
3) \(a=18\), \(b=17\), \(c=5\). Classifique o triângulo quanto a \(\alpha\) (agudo, reto ou obtuso).
4) Em um terreno, lados \(b=24\) m e \(c=31\) m com ângulo compreendido \(\alpha=68^\circ\). Determine o perímetro sabendo que \(a\) é a fachada.
Continue estudando (linkagem interna)
Lei dos Senos — use quando conhece pares lado-ângulo e nos casos SSA/AAS.
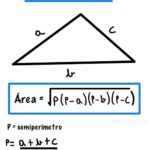
Área do Triângulo — base–altura, 2 lados + ângulo, Heron, circunrádio/inrário.
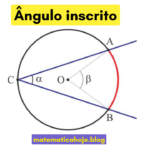
Pontos Notáveis do Triângulo — circuncentro (raio \(R\)) e incentro (raio \(r\)).
Triângulos: tipos e propriedades — classificação e desigualdade triangular.
Trigonometria no triângulo retângulo — revisão de seno, cosseno e tangente.