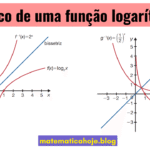
Logaritmo Natural (ln)
O logaritmo natural, também conhecido como logaritmo neperiano, é o logaritmo de base \(e\), onde \(e \approx 2,71828…\) é um número irracional famoso na matemática. Ele é indicado por \(\ln x\) e aparece frequentemente em problemas de crescimento contínuo, juros compostos e cálculo diferencial.

Definição formal
\( \ln x = \log_e x \quad\text{, com } x>0 \)
Isso significa que \(\ln x\) é o expoente ao qual a base \(e\) deve ser elevada para resultar em \(x\).
Por exemplo, \(\ln(e^4)=4\).
Propriedades do Logaritmo Natural
As propriedades do logaritmo natural são as mesmas dos logaritmos em qualquer base, mas com \(a=e\):
1) Logaritmo do produto: \(\ln(xy)=\ln x + \ln y\)
2) Logaritmo do quociente: \(\ln\!\left(\dfrac{x}{y}\right)=\ln x – \ln y\)
3) Logaritmo da potência: \(\ln(x^n)=n\ln x\)
4) Logaritmo da raiz: \(\ln(\sqrt[n]{x})=\dfrac{1}{n}\ln x\)
5) Valor especial: \(\ln 1=0 \quad\text{e}\quad \ln e=1\)
Exemplos resolvidos
Exemplo 1 — Calcular \( \ln e^5 \)
Usando a definição: \[ \ln(e^5)=5 \] Porque \(e^5\) é exatamente a base elevada ao expoente 5. Resposta: 5.
Exemplo 2 — Resolver \( \ln x = 2 \)
Isso significa: \[ \log_e x = 2 \quad \Rightarrow \quad x = e^2 \] Calculando: \[ x \approx 7,389 \] Resposta: \(x=e^2\).
Exemplo 3 — Expandir \( \ln(\sqrt{e^3}) \)
Primeiro, escrevemos a raiz como potência: \[ \sqrt{e^3}=e^{3/2} \] Aplicando a propriedade da potência: \[ \ln(e^{3/2})=\tfrac{3}{2}\ln e \] Como \(\ln e=1\): \[ \ln(\sqrt{e^3})=\tfrac{3}{2}=1,5 \]
Exercícios de múltipla escolha
1) O valor de \( \ln 1 \) é:
- a) 0
- b) 1
- c) \(e\)
- d) Inexistente
Ver resposta
\(\ln 1=0\), pois \(e^0=1\). Alternativa correta: a).
2) Resolver a equação \( \ln x = 3 \).
- a) \(x=e^3\)
- b) \(x=3e\)
- c) \(x=\ln 3\)
- d) \(x=1/e^3\)
Ver resposta
\(\ln x=3 \Rightarrow x=e^3\). Aproximadamente, \(e^3\approx 20,085\). Alternativa correta: a).
3) Qual das alternativas é equivalente a \( \ln\sqrt{e} \)?
- a) \(1/2\)
- b) \(e/2\)
- c) \(\ln e\)
- d) 2
Ver resposta
\(\sqrt{e}=e^{1/2} \Rightarrow \ln(\sqrt{e})=\tfrac{1}{2}\ln e=\tfrac{1}{2}\cdot 1=0,5\). Alternativa correta: a).
4) Usando propriedades, simplifique \( \ln\!\left(\dfrac{e^4}{e^2}\right) \).
- a) 2
- b) 4
- c) 6
- d) 8
Ver resposta
\(\ln(e^4)-\ln(e^2)=4-2=2\). Alternativa correta: a).