Confira questões resolvidas de Matemática da banca IBFC, organizadas e explicadas passo a passo. Ideal para quem busca praticar e entender os padrões dessa banca em concursos. Aperfeiçoe seus estudos com questões de matemática IBFC e melhore seu desempenho!
(Banca IBFC – 2021 – Frações e Números Decimais) O número 1/3 (um terço) em representação decimal assume a forma: 0,33333… com uma infinidade de casas decimais seguintes (repetitivas) com o algarismo 3. Considere o seguinte procedimento para descobrir o par de números que forma uma dízima periódica baseado em uma sequência de operações aritméticas rudimentares e no encadeamento lógico sequencial:
Baseado neste procedimento, analise as afirmativas abaixo e dê valores Verdadeiro (V) ou Falso (F).
( ) 0,999999… = 1
( ) 0,1 + 0,01 + 0,001 + … = 1/9
( ) Um número que não exibe repetição como: 0,123456789101112131415… (onde se encadeiam os inteiros crescentes ao longo de suas casas decimais) pode ter a fração determinada da mesma maneira.
Assinale a alternativa que avalia corretamente as afirmações acima em termos da mesma lógica apresentada no procedimento.
A) F, F, F
B) F, V, V
C) V, V, F
D) F, V, F
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Afirmativa 1: (0,999999\ldots = 1) Essa afirmação é, de fato, verdadeira. Há uma demonstração matemática que comprova que (0,999999\ldots) é igual a 1. Isso pode ser verificado através de um raciocínio semelhante ao apresentado para (0,33333\ldots), onde a dízima periódica representa um valor exato.
Afirmativa 2: 0,1 + 0,01 + 0,001 + … = 1/9 Analisando novamente, esta afirmação também é verdadeira. A soma 0,1 + 0,01 + 0,001 + … forma uma série geométrica infinita com razão (r = 0,1), e a soma de uma série geométrica infinita com (0 < r < 1) é dada por
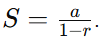
Neste caso:
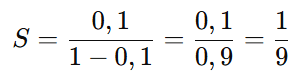
Portanto, a afirmativa é verdadeira.
Afirmativa 3: Um número que não exibe repetição como (0,123456789101112131415…) (onde se encadeiam os inteiros crescentes ao longo de suas casas decimais) pode ter a fração determinada da mesma maneira. Esta afirmação é falsa. Esse tipo de número, que não possui repetição periódica, não é uma dízima periódica e, portanto, não pode ser representado como uma fração. Números com expansões decimais infinitas não periódicas são irracionais e não podem ser expressos como uma fração de dois inteiros.
Conclusão:
Com a análise acima, as afirmações se classificam como:
- Afirmativa 1: Verdadeira
- Afirmativa 2: Verdadeira
- Afirmativa 3: Falsa
Portanto, a alternativa correta é C) V, V, F.
Gostou da explicação? Continue praticando com mais questões matemática IBFC!
[/toggle]
🟣Questões de Matemática IBFC (Nível Fundamental) – PDF Exclusivo para Concursos
🟠Questões de Matemática IBFC (Nível Médio) – PDF Exclusivo para Concursos
🔴Questões de Matemática IBFC (Nível Superior) – PDF Exclusivo para Concursos

























