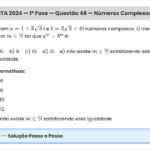
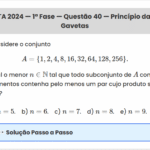
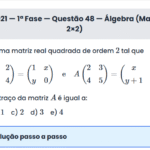
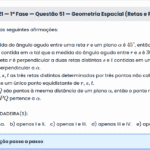
ITA 2020 — 2ª Fase — Questão 4 — Interseção de Funções
Sejam \(a\) e \(b\) dois números reais. Sabendo que o conjunto dos números reais \(k\) para os quais a
reta \(y=kx\) intersecta a parábola \(y=x^2+ax+b\) é igual a \((-\infty,2]\cup[6,+\infty)\),
determine os números \(a\) e \(b\).
👀 Solução passo a passo
A interseção entre a reta \(y=kx\) e a parábola \(y=x^2+ax+b\) é dada pelas soluções de
\[
x^2+ax+b=kx \;\;\Longleftrightarrow\;\; x^2+(a-k)x+b=0. \tag{1}
\]
Para existir interseção, é necessário e suficiente que a equação (1) possua solução real,
isto é, que o discriminante seja não negativo:
\[
\Delta=(a-k)^2-4b\ge 0
\;\;\Longleftrightarrow\;\;
k^2-2ak+a^2-4b\ge 0. \tag{2}
\]
A desigualdade (2) descreve, em \(k\), uma parábola de concavidade para cima; portanto
o conjunto solução é o exterior (com bordas) do intervalo formado por suas raízes. As raízes são
\[
k=a\pm 2\sqrt{b}\quad(\text{com } b\ge 0). \tag{3}
\]
O enunciado informa que o conjunto dos \(k\) que dão interseção é
\((-\infty,2]\cup[6,\infty)\). Logo, o intervalo “proibido” (onde \(\Delta<0\)) é \((2,6)\),
de modo que as raízes de (2) devem ser exatamente \(2\) e \(6\). Assim,
\[
\begin{cases}
a-2\sqrt{b}=2,\\
a+2\sqrt{b}=6.
\end{cases}
\]
Somando, \(2a=8\Rightarrow a=4\). Subtraindo, \(4\sqrt{b}=2\Rightarrow \sqrt{b}=1\Rightarrow b=1\).
Resposta: \(a=4\) e \(b=1\).
🔗 Veja também a questão anterior:
Matemática ITA 2020 — Questão 3 — 2ª Fase