Confira a resolução detalhada de uma questão típica da banca VUNESP. Entenda o método e prepare-se para suas provas com confiança.
(Banca VUNESP – Nível Médio – 2023 – Geometria Plana) Considere um vasilhame com o interior no formato de um paralelepípedo reto retangular, com largura de 9 cm, profundidade de 7 cm, e determinada altura. O volume total do líquido contido nesse vasilhame foi despejado, sem desperdício, em um segundo vasilhame, de mesmo formato interno, sendo a largura, a profundidade e a altura 1 cm maior do que, respectivamente, a largura, a profundidade e a altura do primeiro vasilhame. Sabendo-se que o volume contido no primeiro vasilhame ocupou 63 centésimos do volume total do segundo vasilhame, é correto afirmar que a altura do segundo vasilhame é de
A) 3 cm.
B) 4 cm.
C) 5 cm.
D) 6 cm.
E) 7 cm.
Ver Solução
Geometria – Cálculo do Volume e da Altura
Passo 1: Fórmulas e variáveis
Sabemos que o volume de um paralelepípedo reto retangular é dado por:
V = largura × profundidade × altura
As dimensões do primeiro vasilhame são:
- Largura: 9 cm,
- Profundidade: 7 cm,
- Altura: h1 cm.
O volume do primeiro vasilhame é:
V1 = 9 × 7 × h1 = 63h1
Passo 2: Dimensões do segundo vasilhame
As dimensões do segundo vasilhame são 1 cm maiores:
- Largura: 9 + 1 = 10 cm
- Profundidade: 7 + 1 = 8 cm
- Altura: h2 cm
O volume do segundo vasilhame é:
V2 = 10 × 8 × h2 = 80h2
Passo 3: Relacionar os volumes
O volume do primeiro vasilhame ocupou 63% = 0,63 do volume do segundo:
V1 = 0,63 × V2
Substituímos as expressões de V1 e V2:
63h1 = 0,63 × 80h2
Simplificamos:
63h1 = 50,4h2
Simplificamos:
63h1= 50,4h2
Dividimos ambos os lados por ( h1 ):
h2 = 63h1 /50,4
Passo 4: Determinar a relação entre ( h1 ) e ( h2 )
Sabemos que o líquido foi transferido totalmente. Assim:
h1 = h2 – 1.
Substituímos h1 = h2 – 1 na equação ( h2 = 63h1/50,4 ):
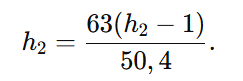
Distribuímos o ( 63 ):
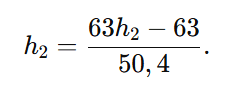
Multiplicamos todos os termos por ( 50,4 ) para eliminar o denominador:
50,4h2 = 63h2 – 63.
Isolamos ( h2 ):
63 – 50,4 = 12,6h2.
Dividimos:
h2 = 63/12,6 = 5.
Resposta
A altura do segundo vasilhame é 5 cm.
Alternativa correta: C) 5 cm.
Gostou desta questão? Confira outras questões resolvidas de Matemática VUNESP aqui.
👉Entre no nosso canal do WhatsApp
Questões Vunesp – Matemática PDF: Prepare-se com Qualidade
🟡Questões Resolvidas de Matemática em PDF da Banca VUNESP – Nível Fundamental
🔵Questões Resolvidas de Matemática em PDF da Banca VUNESP – Nível Médio
🟠Questões Resolvidas de Matemática em PDF da Banca VUNESP – Nível Superior
Raciocínio Lógico Lista em PDF Vunesp
🟣Raciocínio Lógico – Lista de Exercícios Vunesp (Nível Médio)
🟢Raciocínio Lógico – Lista de Exercícios Vunesp (Nível Superior)
🟢Mapas Mentais de Matemática para Concurso