Matriz Transposta
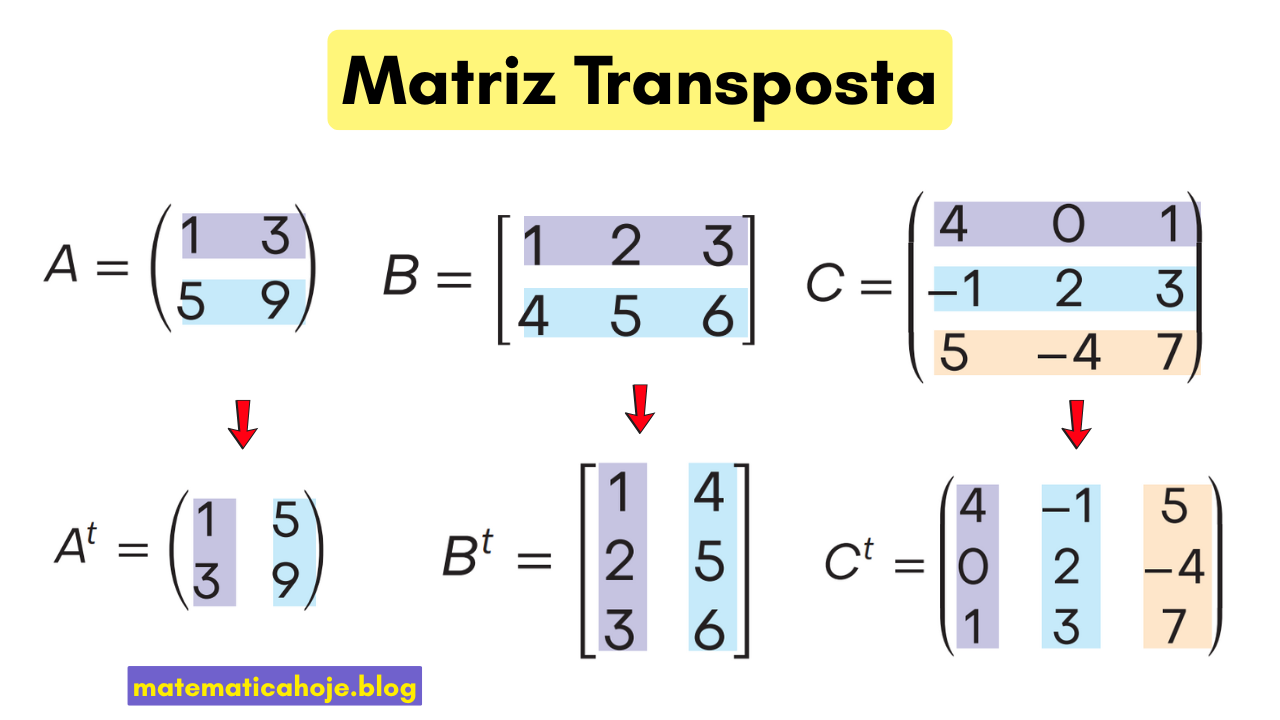
A matriz transposta é obtida a partir de uma matriz qualquer \(A\) trocando suas linhas por colunas. Ou seja, o elemento que estava na posição \((i,j)\) passa para a posição \((j,i)\). A matriz transposta é representada por \(A^T\).
Definição
Dada a matriz \(A = (a_{ij})_{m \times n}\), sua transposta é definida como:
\[ A^T = (a_{ji})_{n \times m} \]
Exemplos
Exemplo 1:
\[ A = \begin{bmatrix} 1 & 3 \\ 5 & 9 \end{bmatrix} \quad \Rightarrow \quad A^T = \begin{bmatrix} 1 & 5 \\ 3 & 9 \end{bmatrix} \]
Exemplo 2:
\[ B = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix} \quad \Rightarrow \quad B^T = \begin{bmatrix} 1 & 4 \\ 2 & 5 \\ 3 & 6 \end{bmatrix} \]
Propriedades da Transposta
- \((A^T)^T = A\)
- \((A+B)^T = A^T + B^T\)
- \((kA)^T = kA^T\), para qualquer escalar \(k\)
- \((AB)^T = B^T A^T\)
Exercícios Resolvidos
1) Calcule a transposta de \(C = \begin{bmatrix}4 & 0 & 1 \\ -1 & 2 & 3 \\ 5 & -4 & 7\end{bmatrix}\).
Ver solução
\[ C^T = \begin{bmatrix} 4 & -1 & 5 \\ 0 & 2 & -4 \\ 1 & 3 & 7 \end{bmatrix} \]
2) Se \(A = \begin{bmatrix}2 & 4 \\ 7 & 1 \\ 3 & 5\end{bmatrix}\), determine \(A^T\).
Ver solução
\[ A^T = \begin{bmatrix} 2 & 7 & 3 \\ 4 & 1 & 5 \end{bmatrix} \]
3) Mostre que \((AB)^T = B^T A^T\) para:
\(A = \begin{bmatrix}1 & 2 \\ 0 & 1\end{bmatrix}, \quad B = \begin{bmatrix}2 & 1 \\ 3 & 4\end{bmatrix}\).
Ver solução
Calculando \(AB\):
\[ AB = \begin{bmatrix} 1\cdot2+2\cdot3 & 1\cdot1+2\cdot4 \\ 0\cdot2+1\cdot3 & 0\cdot1+1\cdot4 \end{bmatrix} = \begin{bmatrix} 8 & 9 \\ 3 & 4 \end{bmatrix} \]
\((AB)^T = \begin{bmatrix}8 & 3 \\ 9 & 4\end{bmatrix}\).
Agora, \(B^T = \begin{bmatrix}2 & 3 \\ 1 & 4\end{bmatrix}, \; A^T = \begin{bmatrix}1 & 0 \\ 2 & 1\end{bmatrix}\).
\[ B^T A^T = \begin{bmatrix}2 & 3 \\ 1 & 4\end{bmatrix} \cdot \begin{bmatrix}1 & 0 \\ 2 & 1\end{bmatrix} = \begin{bmatrix}2\cdot1+3\cdot2 & 2\cdot0+3\cdot1 \\ 1\cdot1+4\cdot2 & 1\cdot0+4\cdot1\end{bmatrix} = \begin{bmatrix}8 & 3 \\ 9 & 4\end{bmatrix} \]
Logo, \((AB)^T = B^T A^T\).