Entender medida de ângulo é fundamental em Geometria, Trigonometria, Física e em questões de provas como Enem e concursos. Neste guia completo, você vai aprender a ler, medir e interpretar ângulos, dando adeus à confusão com graus, minutos, segundos e transferidor.
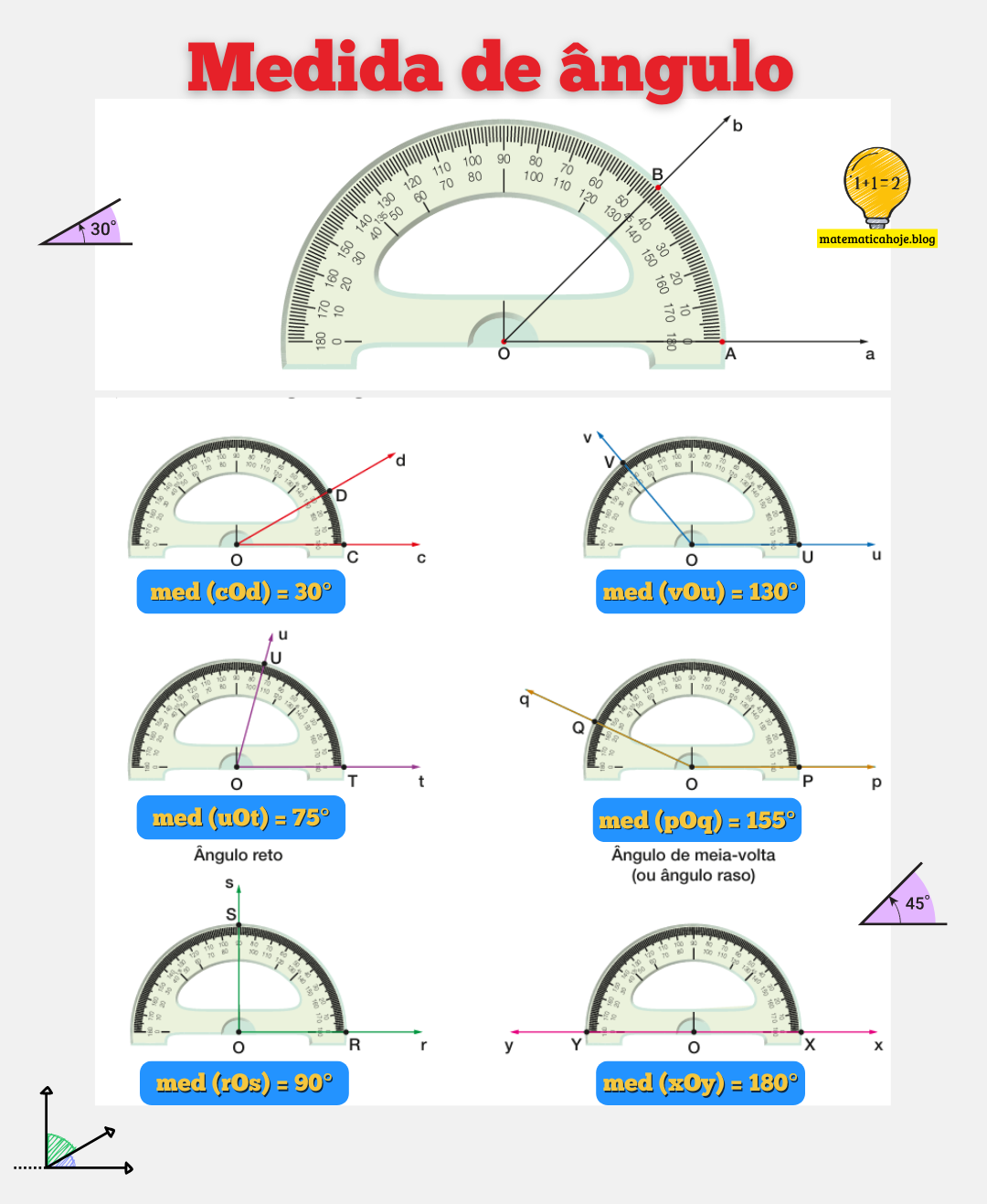
O que é medida de ângulo na prática do dia a dia?
Um ângulo é formado por duas semirretas com a mesma origem (o vértice). A medida do ângulo indica o “tamanho da abertura” entre essas duas semirretas. Quanto maior a abertura, maior a medida do ângulo.
Na prática, você vê ângulos o tempo todo: nos ponteiros do relógio, na abertura de uma porta, na rampa de acesso, nas placas de trânsito, em gráficos de setores e muito mais. Por isso, dominar o conceito de medida de ângulo é essencial para interpretar situações reais e resolver problemas em provas.
A unidade mais usada no Ensino Fundamental e Médio é o grau, representado por \(^{\circ}\). Mas, para medições mais precisas, usamos também minutos (\(‘\)) e segundos (\(”\)), formando o chamado sistema sexagesimal.
Quer todas as fórmulas de Geometria em um só lugar?
Em vez de perder tempo procurando fórmulas de ângulos, áreas e volumes em vários lugares, baixe o eBook gratuito Fórmulas Matemática e tenha um resumo organizado para revisar antes de qualquer prova.
📘 Baixar eBook Fórmulas (Grátis) Ideal para Enem, concursos e provas escolares.Como medir ângulos com o transferidor passo a passo
O transferidor é o instrumento mais usado para medir ângulos em graus. Ele costuma ter uma escala de \(0^{\circ}\) a \(180^{\circ}\) ou de \(0^{\circ}\) a \(360^{\circ}\), dependendo do modelo.
Passo a passo para medir um ângulo com transferidor
- Posicione o centro do transferidor exatamente sobre o vértice do ângulo.
- Alinhe uma das semirretas do ângulo com a marcação zero da escala (linha de base do transferidor).
- Observe onde a outra semirreta corta a escala do transferidor: esse valor é a medida do ângulo em graus.
- Verifique se está usando a escala correta (alguns transferidores possuem duas escalas, crescente e decrescente).
Ao desenhar um ângulo e posicionar o transferidor, a segunda semirreta passa exatamente sobre a marca de \(40^{\circ}\). Logo, a medida do ângulo é:
\[ \text{Medida do ângulo} = 40^{\circ} \]
Esse é um ângulo agudo, pois sua medida está entre \(0^{\circ}\) e \(90^{\circ}\).
Às 12h, os ponteiros do relógio coincidem (ângulo \(0^{\circ}\)). Às 12h15, o ponteiro dos minutos avançou um quarto de volta, enquanto o das horas quase não se moveu.
A abertura observada é de aproximadamente:
\[ \text{Ângulo} \approx 90^{\circ} \]
Ou seja, formamos um ângulo reto.
Se você quiser aprofundar os tipos de ângulos (agudo, reto, obtuso, raso), vale a pena revisar o artigo completo do Matemática Hoje sobre ângulos agudo, obtuso, reto e raso .
Graus, minutos e segundos: sistema sexagesimal em detalhes
No sistema sexagesimal, a unidade principal é o grau. Quando precisamos de mais precisão, dividimos o grau em partes menores:
- \(1^{\circ} = 60’\) (60 minutos)
- \(1′ = 60”\) (60 segundos)
- Logo, \(1^{\circ} = 3600”\) (60 × 60)
Como ler uma medida com graus, minutos e segundos
Veja a medida \(35^{\circ} 20′ 10”\). Lemos assim: “trinta e cinco graus, vinte minutos e dez segundos”.
Transforme \(45’\) em graus.
Sabemos que:
\[ 1^{\circ} = 60′ \\ 45′ = x^{\circ} \]
Aplicando proporção:
\[ x^{\circ} = \frac{45′}{60′} \\ x^{\circ} = \frac{45}{60} \\ x^{\circ} = \frac{3}{4} = 0{,}75^{\circ} \]
Transforme \(900”\) em graus.
\[ 1^{\circ} = 3600” \\ 900” = x^{\circ} \]
\[ x^{\circ} = \frac{900}{3600} \\ x^{\circ} = \frac{1}{4} = 0{,}25^{\circ} \]
Logo, \(900” = 0{,}25^{\circ}\).
Em provas mais avançadas, aparece também o radiano, unidade padrão de medida de ângulos no Sistema Internacional. Mas, no ensino básico, a maior parte das questões usa apenas graus, minutos e segundos.
Mapa mental de ângulos para revisão rápida
Se você gosta de aprender visualmente, um mapa mental reúne, em uma só folha, tipos de ângulos, medidas, propriedades e exemplos. Perfeito para revisar antes da prova.
🧠 Ver Mapas Mentais de Matemática Use junto com este artigo para fixar os principais conceitos.Tipos de ângulos e relações mais cobradas em provas
Além da medida individual de cada ângulo, provas como Enem e concursos exploram bastante os tipos de ângulos e as relações entre eles.
Principais tipos de ângulos
- Ângulo nulo: \(0^{\circ}\)
- Ângulo agudo: entre \(0^{\circ}\) e \(90^{\circ}\)
- Ângulo reto: \(90^{\circ}\)
- Ângulo obtuso: entre \(90^{\circ}\) e \(180^{\circ}\)
- Ângulo raso: \(180^{\circ}\)
- Ângulo completo: \(360^{\circ}\)
Ângulos complementares e suplementares
- Complementares: a soma das medidas é \(90^{\circ}\). Se os ângulos medem \(\alpha\) e \(\beta\), então: \[ \alpha + \beta = 90^{\circ} \]
- Suplementares: a soma das medidas é \(180^{\circ}\). \[ \alpha + \beta = 180^{\circ} \]
Qual é o ângulo complementar de \(32^{\circ}\)?
\[ x + 32^{\circ} = 90^{\circ} \\ x = 90^{\circ} – 32^{\circ} \\ x = 58^{\circ} \]
Logo, o ângulo complementar de \(32^{\circ}\) mede \(58^{\circ}\).
Qual é o ângulo suplementar de \(110^{\circ}\)?
\[ x + 110^{\circ} = 180^{\circ} \\ x = 180^{\circ} – 110^{\circ} \\ x = 70^{\circ} \]
Portanto, o ângulo suplementar de \(110^{\circ}\) mede \(70^{\circ}\).
Para um estudo mais completo, veja também o artigo: Ângulos: como resolver tudo sem errar no Enem .
Exemplos resolvidos de medida de ângulo em questões
Enunciado: Em um relógio analógico, qual é a medida, em graus, do ângulo formado entre os ponteiros às 3 horas em ponto?
Resolução:
Em uma volta completa temos \(360^{\circ}\) e 12 horas. Cada “salto” de uma hora corresponde a:
\[ \frac{360^{\circ}}{12} = 30^{\circ} \]
Às 3h, o ponteiro das horas aponta para o 3 e o dos minutos para o 12. A diferença entre o 12 e o 3 é de 3 intervalos:
\[ \text{Ângulo} = 3 \cdot 30^{\circ} \\ \text{Ângulo} = 90^{\circ} \]
Formamos um ângulo reto.
Enunciado: Em certa figura, dois ângulos são complementares. Um deles mede \(x^{\circ}\) e o outro mede \(2x^{\circ}\). Encontre o valor de \(x\).
Resolução:
Se são complementares:
\[ x^{\circ} + 2x^{\circ} = 90^{\circ} \\ 3x^{\circ} = 90^{\circ} \\ x^{\circ} = \frac{90^{\circ}}{3} \\ x^{\circ} = 30^{\circ} \]
Assim, o primeiro ângulo mede \(30^{\circ}\) e o segundo mede \(60^{\circ}\).
Quer treinar ângulos junto com outros temas que caem em provas? Veja o guia geral de Matemática para o Enem e os materiais completos de 10 eBooks de Matemática .
Lista de exercícios sobre medida de ângulos comentados
Resolva os exercícios a seguir antes de abrir a solução. Em seguida, compare seu raciocínio com o passo a passo.
Exercício 1 – Ângulo complementar em situação de prova
Em um exercício de geometria, um dos ângulos de uma figura mede \(35^{\circ}\) e o outro é seu complementar. Qual é a medida desse outro ângulo?
Se os ângulos são complementares, a soma de suas medidas é \(90^{\circ}\).
\[ 35^{\circ} + x = 90^{\circ} \]
Isolando \(x\):
\[ x = 90^{\circ} – 35^{\circ} \\ x = 55^{\circ} \]
Portanto, o ângulo complementar de \(35^{\circ}\) mede \(55^{\circ}\).
Exercício 2 – Ângulos suplementares em figura geométrica
Dois ângulos formam um par suplementar. Um mede \(112^{\circ}\). Calcule a medida do outro.
Em ângulos suplementares, a soma das medidas é \(180^{\circ}\).
\[ 112^{\circ} + x = 180^{\circ} \]
Isolando \(x\):
\[ x = 180^{\circ} – 112^{\circ} \\ x = 68^{\circ} \]
Logo, o outro ângulo mede \(68^{\circ}\).
Exercício 3 – Conversão de minutos para graus
Um determinado ângulo mede \(150’\) (minutos). Qual é essa medida em graus?
Sabemos que \(1^{\circ} = 60’\). Logo:
\[ 150′ = x^{\circ} \]
A conversão é:
\[ x^{\circ} = \frac{150′}{60′} \\ x^{\circ} = \frac{150}{60} \\ x^{\circ} = \frac{5}{2} = 2{,}5^{\circ} \]
Portanto, o ângulo de \(150’\) corresponde a \(2{,}5^{\circ}\).
Exercício 4 – Conversão de graus em graus, minutos e segundos
Escreva \(36{,}25^{\circ}\) na forma \(^{\circ}\), \(‘\) e \(”\).
A parte inteira é \(36^{\circ}\). A parte decimal \(0{,}25^{\circ}\) será convertida em minutos.
\[ 0{,}25^{\circ} \cdot 60 = 15′ \]
Não sobrou parte decimal nos minutos, então não há segundos.
Assim:
\[ 36{,}25^{\circ} = 36^{\circ} 15′ \]
Logo, a medida do ângulo é \(36^{\circ} 15’\).
Exercício 5 – Aplicando medida de ângulo em triângulo retângulo
Em um triângulo retângulo, um dos ângulos agudos mede \(38^{\circ}\). Qual é a medida do outro ângulo agudo?
Em qualquer triângulo, a soma dos ângulos internos é \(180^{\circ}\). Em um triângulo retângulo, um dos ângulos mede \(90^{\circ}\).
Seja \(x^{\circ}\) a medida do outro ângulo agudo:
\[ 90^{\circ} + 38^{\circ} + x^{\circ} = 180^{\circ} \]
\[ 128^{\circ} + x^{\circ} = 180^{\circ} \]
\[ x^{\circ} = 180^{\circ} – 128^{\circ} \\ x^{\circ} = 52^{\circ} \]
Portanto, o outro ângulo agudo mede \(52^{\circ}\).
Para aprofundar triângulo retângulo, consulte: artigo de triângulo retângulo no Matemática Hoje .
Quer mais questões comentadas de geometria e outros conteúdos? Acesse o banco de questões de Matemática do Matemática Hoje.
Conclusão: como dominar medida de ângulo para qualquer prova
Ao longo deste artigo, você viu que medida de ângulo vai muito além de decorar nomes. Entendeu o que é um ângulo, como usar o transferidor, como funcionam graus, minutos e segundos e quais são as principais relações cobradas, como ângulos complementares e suplementares.
Para consolidar o conteúdo, o caminho é simples: refazer os exemplos, treinar a lista de exercícios e, se possível, criar seus próprios problemas com situações do cotidiano (relógio, placas, dobradiças, rampas, etc.). Assim, o tema deixa de ser abstrato e passa a fazer sentido.
Combine este resumo com o eBook de fórmulas, mapas mentais e listas de questões do Matemática Hoje e você estará muito mais seguro para enfrentar provas do Ensino Fundamental, Médio, Enem e concursos públicos.
FAQ – Perguntas frequentes sobre medida de ângulo
Qual é a diferença entre ângulo agudo, reto, obtuso e raso?
O ângulo agudo tem medida menor que \(90^{\circ}\). O ângulo reto mede exatamente \(90^{\circ}\). O obtuso está entre \(90^{\circ}\) e \(180^{\circ}\). Já o raso mede exatamente \(180^{\circ}\), ou seja, corresponde a meia volta.
Quando usar graus, minutos e segundos na medida de ângulo?
Usamos somente graus em situações mais simples e em muitas questões escolares. Minutos e segundos aparecem quando precisamos de maior precisão na medida, como em navegação, astronomia, topografia e problemas mais detalhados de geometria e trigonometria.
O que significa dizer que dois ângulos são complementares?
Dois ângulos são complementares quando a soma de suas medidas é \(90^{\circ}\). Em geral, as questões apresentam a medida de um dos ângulos e pedem a medida do outro, bastando fazer a diferença \(90^{\circ}\) menos a medida conhecida.
Como a medida de ângulo aparece em questões do Enem?
No Enem, a medida de ângulo costuma aparecer em contextos de figuras planas, relógios, rampas, placas, triângulos e problemas de interpretação geométrica. Geralmente, o foco está em relacionar a medida angular à situação descrita, e não apenas em cálculos mecânicos.
Sobre o autor
Artigo escrito por Adriano Rocha, professor de Matemática, especialista em ensino por resolução de problemas e criador do blog Matemática Hoje, focado em Enem, concursos e reforço escolar.













