Multiplicação de Matriz por Número Real (Escalar)
A multiplicação de uma matriz por um número real — também chamada de multiplicação por escalar — é uma operação elementar que aparece com frequência no ENEM e em concursos. Se você está organizando seus estudos, confira os Mapas Mentais de Matemática e o Banco de Questões.
Definição
Seja \(k \in \mathbb{R}\) e \(A=(a_{ij})\) uma matriz de ordem \(m\times n\). Definimos \(kA=(ka_{ij})\) como a matriz obtida multiplicando cada elemento de \(A\) pelo escalar \(k\).
Exemplo passo a passo
Considere a matriz
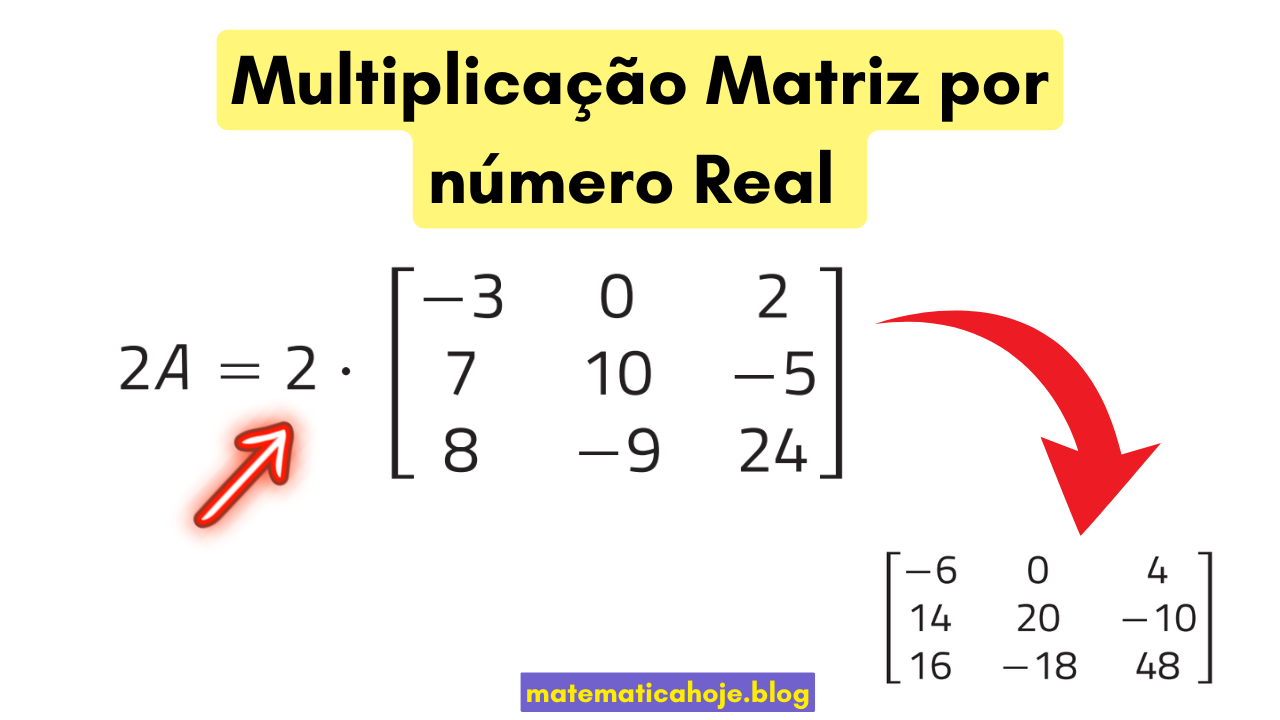
\( A=\begin{bmatrix} -3 & 0 & 2\\ 7 & 10 & -5\\ 8 & -9 & 24 \end{bmatrix}. \quad \) Calcular \(2A\):
\( 2A=\begin{bmatrix} 2(-3) & 2\cdot0 & 2\cdot2\\ 2\cdot7 & 2\cdot10 & 2(-5)\\ 2\cdot8 & 2(-9) & 2\cdot24 \end{bmatrix} =\begin{bmatrix} -6 & 0 & 4\\ 14 & 20 & -10\\ 16 & -18 & 48 \end{bmatrix}. \)
Propriedades úteis
- Distributiva na soma de matrizes: \(k(A+B)=kA+kB\).
- Distributiva na soma de escalares: \((k+\lambda)A=kA+\lambda A\).
- Associativa com escalar: \(k(\lambda A)=(k\lambda)A\).
- Elemento neutro multiplicativo: \(1\cdot A=A\).
- Escalar zero: \(0\cdot A=\mathbf{0}\) (matriz nula).
- Escalar \(-1\): \((-1)\cdot A=-A\) (gera a matriz oposta).
Exercícios Resolvidos
Exercício 1: Calcule \( -3A \) para \( A=\begin{bmatrix} 2 & -1\\ 0 & \tfrac{1}{2} \end{bmatrix}. \)
Mostrar solução
\( -3A=\begin{bmatrix} -6 & 3\\ 0 & -\tfrac{3}{2} \end{bmatrix}. \)
Exercício 2: Mostre que \( 2(A+B)=2A+2B \) usando
\( A=\begin{bmatrix} 1 & 4\\ -2 & 0 \end{bmatrix},\quad B=\begin{bmatrix} 3 & -1\\ 5 & 2 \end{bmatrix}. \)
Mostrar solução
\(A+B=\begin{bmatrix} 4 & 3\\ 3 & 2 \end{bmatrix}\Rightarrow
2(A+B)=\begin{bmatrix} 8 & 6\\ 6 & 4 \end{bmatrix}.\)
\(2A=\begin{bmatrix} 2 & 8\\ -4 & 0 \end{bmatrix},\;
2B=\begin{bmatrix} 6 & -2\\ 10 & 4 \end{bmatrix}\Rightarrow
2A+2B=\begin{bmatrix} 8 & 6\\ 6 & 4 \end{bmatrix}.\)
Igualdade verificada.
Exercício 3: Encontre \(k\) tal que \(kA=\begin{bmatrix} -12 & 6\\ 8 & -4 \end{bmatrix}\), sabendo que \(A=\begin{bmatrix} 6 & -3\\ 4 & -2 \end{bmatrix}\).
Mostrar solução
Compare uma entrada: \(k\cdot 6=-12 \Rightarrow k=-2\). Checando as demais entradas, o valor confere. Logo, \(k=-2\).
Para continuar estudando
Amplie seu domínio em matrizes e esteja pronto para as provas:





















