Estudar múltiplos e divisores é fundamental para desenvolver uma compreensão sólida dos números e suas propriedades, além de facilitar a resolução de problemas em diversas áreas da matemática. Neste material, apresentamos uma lista de exercícios com soluções detalhadas, abordando conceitos essenciais como divisibilidade, números primos, fatoração, múltiplos e o mínimo múltiplo comum (MMC), divisores e o máximo divisor comum (MDC). A proposta é fortalecer o entendimento e a aplicação prática de cada tópico, fornecendo explicações passo a passo para facilitar o aprendizado.
Esses exercícios são organizados de forma progressiva para ajudar tanto na identificação de múltiplos e divisores, quanto na resolução de problemas que envolvem cálculos com MMC e MDC. Então, prepare-se para colocar em prática os conceitos e ganhar confiança para enfrentar desafios mais complexos!
01 – (Ufscar-SP) Um determinado corpo celeste é visível da Terra a olho nu de 63 em 63 anos, tendo sido visto pela última vez no ano de
De acordo com o calendário atualmente em uso, o primeiro ano da Era Cristã em que esse corpo celeste esteve visível a olho nu da Terra foi no ano:
a) 15
b) 19
c) 23
d) 27
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
02 – Ache o maior número de 4 algarismos que é divisível por 13 e o menor número natural de 4 algarismos que é divisível por 17. A diferença entre os resultados é um número:
a) primo.
b) múltiplo de 6.
c) menor que 5 000.
d) divisível por 5.
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
03 – 6__41 representa um número de quatro algarismos. Esse número deve ser divisível por Quantas são as possibilidades para o algarismo desconhecido, representado por __?
a) uma
b) duas
c) três
d) quatro
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
04 – Qual é o menor número natural divisível por 6 que se escreve usando apenas os algarismos 1 e 0?
Esse número dividido por 4 deixa resto:
a) 0
b) 1
c) 2
d) 3
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
05 – (IFCE) O algarismo que se deve intercalar entre os algarismos do número 76 de modo que o número obtido seja divisível por 4 e 9 simultaneamente é:
a) 1
b) 7
c) 5
d) 6
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
06 – Babilônia é um pequeno distrito da cidade de Delfinópolis (MG). Vamos supor que uma rua de Babilônia tenha apenas 8 casas, numeradas por 7, 12, 19, 25, 31, 39, 46 e 53. Adicionando os números das casas que são números primos, obtemos:
a) 110
b) 88
c) 79
d) 57
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
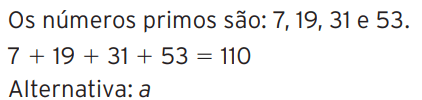
[/toggle]
07 – O número de três algarismos 41__ deve ser primo. Quantas são as possibilidades para o algarismo desconhecido, representado por __?
a) nenhuma
b) uma
c) duas
d) três
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
08 – A soma de três números naturais consecutivos é sempre um número:
a) par.
b) ímpar.
c) primo.
d) múltiplo de 3.
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
09 – (Obmep) O número 4 580 254 é múltiplo de 7. Qual dos números abaixo também é múltiplo de 7?

a) 4 580 249
b) 4 580 248
c) 4 580 247
d) 4 580 246
e) 4 580 245
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
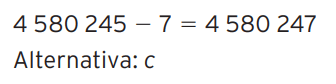
[/toggle]
10 – (Obmep) Isabel escreveu em seu caderno o maior número de três algarismos que é múltiplo de 13. Qual é a soma dos algarismos do número que ela escreveu?
a) 23
b) 24
c) 25
d) 26
e) 27
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
11 – (Saresp) Dentre os números 56, 45, 40 e 35, aquele que é múltiplo de 4 e 7 é
a) 56.
b) 45.
c) 40.
d) 35
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]

























