O Cubo: Propriedades e Fórmulas Essenciais

O cubo é um sólido geométrico fascinante, conhecido por suas faces quadradas e propriedades simétricas. Sendo um caso especial de prisma e paralelepípedo, o cubo possui características únicas que o tornam um dos sólidos mais estudados na geometria. Neste artigo, vamos explorar as principais propriedades do cubo, abordando sua área total, volume, diagonal da face e diagonal do cubo.

Planificação do cubo
Quantas faces tem um cubo
Quantas arestas tem um cubo
Que formato tem cada face do cubo
Quantas vértices tem um cubo
Volume do cubo
Diagonal do cubo fórmula
Planificação do cubo para imprimir

Área Total do Cubo

A área total de um cubo é a soma das áreas de todas as suas seis faces. Como cada face do cubo é um quadrado e todas as faces são congruentes, a área total pode ser facilmente calculada. Se o lado do cubo é representado por (a), a área de uma única face é (a^2). Portanto, a área total A_t é dada por:

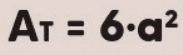
Essa fórmula indica que a área total é proporcional ao quadrado do comprimento do lado do cubo, multiplicada pelo número de faces, que é 6.

Volume do Cubo

O volume de um cubo representa o espaço tridimensional que ele ocupa. Como todas as três dimensões do cubo são iguais (comprimento, largura e altura), o volume V pode ser calculado elevando o comprimento do lado (a) ao cubo:

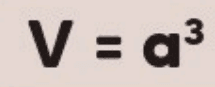
Essa fórmula mostra que o volume do cubo cresce exponencialmente à medida que o comprimento do lado aumenta.

Diagonal da Face do Cubo

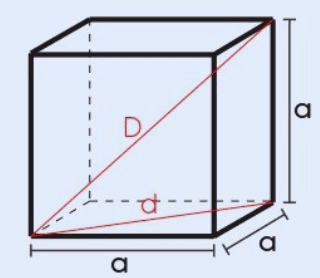
A diagonal da face do cubo é a linha que liga dois vértices opostos de uma de suas faces quadradas. Como cada face é um quadrado, podemos usar o Teorema de Pitágoras para calcular o comprimento dessa diagonal (d_f). Se o lado do cubo é (a), a diagonal da face é dada por:

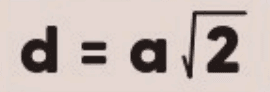
Esta fórmula revela que a diagonal da face é a raiz quadrada de 2 vezes o comprimento do lado do cubo.

Diagonal do Cubo

A diagonal do cubo é a linha que liga dois vértices opostos, passando pelo interior do cubo. Essa diagonal atravessa o cubo, conectando vértices que não compartilham uma mesma face. Para calcular o comprimento da diagonal do cubo (d_c), usamos o Teorema de Pitágoras em três dimensões. Se o lado do cubo é (a), a diagonal do cubo é dada por:

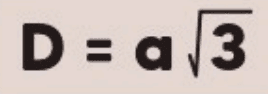
Essa fórmula indica que a diagonal do cubo é a raiz quadrada de 3 vezes o comprimento do lado, mostrando que ela é mais longa que a diagonal de uma única face.

Conclusão

O cubo é uma figura geométrica essencial que combina simplicidade e simetria com propriedades matemáticas importantes. A compreensão de conceitos como área total, volume, diagonal da face e diagonal do cubo é fundamental para explorar mais profundamente a geometria e suas aplicações práticas. Essas fórmulas não apenas permitem calcular dimensões específicas do cubo, mas também fornecem uma base sólida para o estudo de outros sólidos geométricos e suas propriedades relacionadas.

Cilindro: Conceitos e Cálculos

Tronco de Pirâmide: Propriedades, Fórmulas e Proporções

Exercícios de Poliedros: Teste Seu Conhecimento Geométrico

"Artigo escrito por"

Adriano Rocha

Sou Adriano Rocha, professor de Matemática com mestrado e especialização em Resolução de Problemas, além de expertise em concursos públicos. Leciono no Colégio Estadual Mimoso do Oeste e utilizo metodologias inovadoras para aprimorar a compreensão matemática e a resolução de problemas. Produzo conteúdos como artigos para blogs, livros, eBooks e mapas mentais, além de desenvolver materiais didáticos e participar de eventos acadêmicos, sempre com o objetivo de contribuir para o ensino e aprendizagem da Matemática.