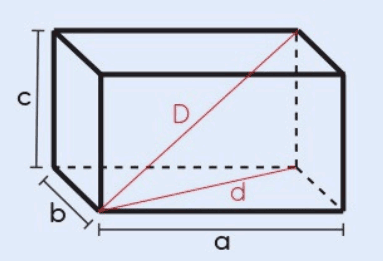
O paralelepípedo é um sólido geométrico tridimensional da matemática com faces retangulares, amplamente utilizado em várias áreas práticas como arquitetura e engenharia. Neste artigo, exploraremos as principais propriedades desse sólido, focando na área total, volume, diagonal da face e diagonal do paralelepípedo, utilizando as notações (a), (b) e (c) para as arestas, (D) para a diagonal do paralelepípedo e (d) para a diagonal da base.
Área Total do Paralelepípedo
A área total de um paralelepípedo é a soma das áreas de todas as suas seis faces. Como as faces opostas são retângulos congruentes, a área total (At) é calculada somando as áreas dos três pares de faces opostas. Se as arestas têm comprimentos (a), (b) e (c), a área total é dada por:
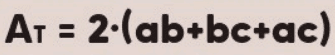
Essa fórmula reflete a soma das áreas das três dimensões distintas multiplicada por 2 para incluir todas as seis faces.
Volume do Paralelepípedo
O volume do paralelepípedo, que representa o espaço tridimensional que ele ocupa, é dado pelo produto das três dimensões (a), (b) e (c):

Esta fórmula mostra que o volume é determinado pelo produto direto das arestas do paralelepípedo.
Diagonal da Face do Paralelepípedo
A diagonal da face do paralelepípedo, indicada por (d), é a linha que conecta dois vértices opostos de uma das faces retangulares. Utilizando o Teorema de Pitágoras, a diagonal da face com lados (a) e (b) é calculada como:

Da mesma forma, para outras faces, as diagonais são dadas por √a2 + c2 ou √b2 + c2, dependendo das arestas que formam a face.
Diagonal do Paralelepípedo
A diagonal do paralelepípedo, indicada por (D), é a linha que conecta dois vértices opostos, passando pelo interior do sólido. Ela é calculada usando o Teorema de Pitágoras em três dimensões, envolvendo as três arestas (a), (b) e (c):

Essa fórmula mostra que a diagonal do paralelepípedo é influenciada por todas as dimensões do sólido e é sempre maior do que as diagonais de suas faces.

Conclusão
O paralelepípedo é uma figura geométrica fundamental, com várias propriedades importantes. Compreender sua área total, volume, diagonal da face e diagonal do paralelepípedo é essencial para resolver problemas geométricos e aplicar esses conceitos em contextos práticos. Essas fórmulas fornecem uma base sólida para explorar a geometria tridimensional e suas aplicações.
Leia também
O Cubo: Propriedades e Fórmulas Essenciais
O Paralelepípedo: Propriedades e Fórmulas Essenciais
Pirâmides: Propriedades, Fórmulas e Aplicações
Tetraedro Regular: Propriedades, Fórmulas e Aplicações
Tronco de Pirâmide: Propriedades, Fórmulas e Proporções
Cilindro: Conceitos e Cálculos
Cone: Tudo o Que Você Precisa Saber
Poliedros: Estrutura, Teorema de Euler e Poliedros de Platão













