Confira a resolução detalhada das questões da OBMEP 2024 – Segunda Fase – Nível 1, da questão 1 à 6. Cada problema é analisado com explicações passo a passo, imagens ilustrativas, estrutura HTML responsiva e sistema de abre e fecha colorido para facilitar a leitura. Ideal para alunos, professores e olimpianos que desejam revisar o conteúdo com clareza e estratégia.
🧠 Mapas Mentais de MatemáticaQuestão 01. Cláudia disse para Marco:
Escolha um planeta da figura ao lado. Vou fazer quatro perguntas e descobrir o planeta que você escolheu. Você deve responder SIM ou NÃO a cada pergunta, na ordem em que eu perguntar. Você pode mentir em todas as respostas ou falar a verdade em todas as respostas.
As perguntas são:
- O nome do planeta que você escolheu tem 5 letras?
- O nome do planeta que você escolheu tem a letra F?
- O nome do planeta que você escolheu tem as letras M ou S?
- O nome do planeta que você escolheu tem a letra N?
a) Se Marco escolher Saturno e decidir sempre mentir, quais respostas ele deve dar?
(Responda usando SIM ou NÃO)
1. _______
2. _______
3. _______
4. _______
b) Qual das quatro perguntas permite descobrir se Marco decidiu sempre mentir ou sempre dizer a verdade? Justifique sua resposta.
c) Suponha que Marco tenha escolhido um planeta e respondido, na ordem, as seguintes respostas: SIM, SIM, NÃO, NÃO. Qual foi o planeta escolhido? Justifique.

🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Marco escolheu Saturno e decidiu mentir em todas as respostas. Vamos analisar cada pergunta com base nas características do planeta Saturno.
1) O nome do planeta tem 5 letras?
Saturno tem 7 letras, então a resposta verdadeira seria NÃO. Como Marco mente, ele responderá:
$$ \text{SIM} $$
2) O nome do planeta tem a letra F?
Saturno não tem a letra F. A resposta verdadeira seria NÃO. Mentindo, ele responderá:
$$ \text{SIM} $$
3) O nome do planeta tem as letras M ou S?
Saturno tem a letra S. A resposta verdadeira seria SIM. Mentindo, ele responderá:
$$ \text{NÃO} $$
4) O nome do planeta tem a letra N?
Saturno tem a letra N. A resposta verdadeira seria SIM. Mentindo, ele responderá:
$$ \text{NÃO} $$
✅ Conclusão do item a):
- Respostas de Marco:
- 1. SIM
- 2. SIM
- 3. NÃO
- 4. NÃO
🔎 Item b) Qual pergunta permite saber se Marco está mentindo ou dizendo a verdade?
A segunda pergunta é a chave: “O nome do planeta tem a letra F?”
Nenhum planeta do sistema solar tem a letra F no nome. Ou seja:
- Se Marco responder SIM, ele está mentindo.
- Se responder NÃO, está dizendo a verdade.
✅ Conclusão do item b):
- A segunda pergunta revela se Marco está mentindo ou dizendo a verdade.
🔎 Item c) Com base na resposta SIM da segunda pergunta, qual é o planeta escolhido?
Se a resposta foi SIM para a 2ª pergunta, Marco está mentindo. Sabendo disso, podemos usar as demais respostas para descobrir qual planeta possui as características contrárias às respostas dadas.
Marco respondeu: SIM, SIM, NÃO, NÃO
Como ele mentiu, as respostas verdadeiras seriam: NÃO, NÃO, SIM, SIM
Então o planeta escolhido:
- Não tem 5 letras
- Não tem a letra F
- Tem M ou S
- Tem a letra N
A única opção que satisfaz esses critérios é MARTE.
| Planeta | 5 Letras | Tem F? | Tem M ou S? | Tem N? |
|---|---|---|---|---|
| Marte | SIM | NÃO | SIM | NÃO |
| Saturno | NÃO | NÃO | SIM | SIM |
| Vênus | SIM | NÃO | SIM | SIM |
✅ Conclusão do item c):
- O planeta escolhido é: MARTE
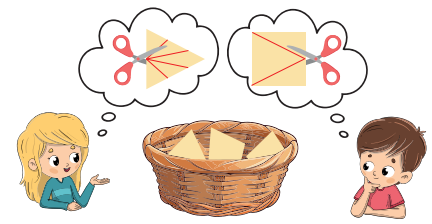
Questão 02. Ana e Pedro cortam pedaços de papel que estão em uma cesta.
- Sempre que Ana pega um pedaço, corta em cinco pedaços e devolve todos os pedaços cortados para a cesta.
- Sempre que Pedro pega um pedaço, corta em três pedaços e devolve todos os pedaços cortados para a cesta.
- Inicialmente, há três pedaços de papel na cesta.
a) Quantos pedaços de papel ficarão na cesta depois de Ana e Pedro pegarem um pedaço cada um e devolverem os pedaços cortados para a cesta?
b) Descreva uma maneira de Ana e Pedro pegarem, cortarem e devolverem todos os pedaços de papel da cesta de modo que, a partir dos três pedaços iniciais, a cesta fique com 11 pedaços.
c) Explique por que, a partir dos três pedaços iniciais, a cesta nunca ficará com 2024 pedaços após Ana e Pedro devolverem todos os pedaços cortados para a cesta.
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
O objetivo é acompanhar o crescimento do número de pedaços de papel, conforme Ana e Pedro vão realizando ações. Precisamos entender como cada ação afeta a quantidade total na cesta.
1) Resolvendo o item a:
Vamos analisar o efeito das ações de Ana e Pedro individualmente:
- Ana: pega 1 pedaço, corta em 5, devolve 5 → a cesta ganha +4 pedaços (5 – 1)
- Pedro: pega 1 pedaço, corta em 3, devolve 3 → a cesta ganha +2 pedaços (3 – 1)
Logo, se ambos realizarem essas ações a partir de 3 pedaços iniciais:
$$ 3 + 4 + 2 = 9 \text{ pedaços} $$
✅ Conclusão do item a):
- Após uma ação de Ana e uma de Pedro, a cesta terá 9 pedaços de papel.
2) Resolvendo o item b:
Nosso objetivo é alcançar 11 pedaços a partir de 3 pedaços iniciais, usando ações de Ana e Pedro. Como cada ação aumenta a quantidade de papéis, vamos buscar sequências cujos ganhos somem 8 (pois 3 + 8 = 11).
Como vimos:
- Cada ação de Ana: +4 pedaços
- Cada ação de Pedro: +2 pedaços
Vamos encontrar combinações de somas que resultem em +8:
- 2 vezes Ana: 4 + 4 = 8
- Ana, Pedro, Pedro: 4 + 2 + 2 = 8
- Pedro, Ana, Pedro: 2 + 4 + 2 = 8
- Pedro, Pedro, Ana: 2 + 2 + 4 = 8
- Pedro, Ana, Ana: 2 + 4 + 4 = 10 (excede)
Exemplo de sequência válida:
- Ana → Pedro → Pedro: 3 → 7 → 9 → 11
✅ Conclusão do item b):
- Uma sequência possível é: Ana → Pedro → Pedro, entre outras variações que totalizam +8 pedaços.
3) Resolvendo o item c:
Vamos observar a paridade (par ou ímpar) da quantidade de pedaços:
- Inicialmente, há 3 pedaços: número ímpar
- Ação de Ana: adiciona 4 (par) → ímpar + par = ímpar
- Ação de Pedro: adiciona 2 (par) → ímpar + par = ímpar
Ou seja, após qualquer sequência de ações, o total de pedaços continuará sendo um número ímpar.
Como 2024 é par, nunca será atingido.
✅ Conclusão do item c):
- A quantidade de papéis na cesta será sempre ímpar, então nunca será igual a 2024.
Questão 03. A figura ao lado é formada por quadrados e triângulos. O lado do quadrado vermelho mede 2 cm. Os demais quadrados e triângulos têm lados paralelos a um dos lados ou a uma das diagonais do quadrado vermelho.
a) Qual é a área da região amarela?
b) Qual é a área da região branca?
c) Qual é a área da região cinza?

🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Vamos decompor a figura em regiões menores usando uma malha quadriculada baseada nos lados e diagonais do quadrado vermelho. Essa malha facilita a contagem e o cálculo das áreas.
1) Item a) – Área da região amarela:
O quadrado vermelho tem lado 2 cm, então sua área é:
$$ 2 \times 2 = 4 \text{ cm}^2 $$
Ao redor dele há 4 quadrados (um em cada lado), e cada um foi dividido em 4 triângulos iguais. Entre esses, 1 é amarelo.
Logo, a área de cada triângulo amarelo é:
$$ \frac{1}{4} \times 4 = 1 \text{ cm}^2 $$
Como temos 4 triângulos amarelos:
$$ 4 \times 1 = 4 \text{ cm}^2 $$
✅ Conclusão do item a):
- A área da região amarela é 4 cm².
2) Item b) – Área da região branca:
Há dois tipos de triângulos brancos:
- 4 pequenos, com área igual à dos amarelos: $$ 1 \text{ cm}^2 $$
- 2 grandes, equivalentes à metade do quadrado vermelho: $$ \frac{1}{2} \times 4 = 2 \text{ cm}^2 $$
Soma das áreas:
$$ 4 \times 1 + 2 \times 2 = 4 + 4 = 8 \text{ cm}^2 $$
✅ Conclusão do item b):
- A área da região branca é 8 cm².
3) Item c) – Área da região cinza:
A região cinza é formada por:
- 4 quadrados verdes, cada um com área igual à do quadrado vermelho: $$ 4 \text{ cm}^2 $$
- 12 triângulos azuis, com área igual à dos triângulos amarelos: $$ 1 \text{ cm}^2 $$
Soma das áreas:
$$ 4 \times 4 + 12 \times 1 = 16 + 12 = 28 \text{ cm}^2 $$
Por fim, somamos os triângulos cinzas (2 deles), com área igual à metade do quadrado vermelho:
$$ 2 \times 2 = 4 \text{ cm}^2 $$
Total:
$$ 28 + 4 + 8 = 40 \text{ cm}^2 $$
✅ Conclusão do item c):
- A área da região cinza é 40 cm².
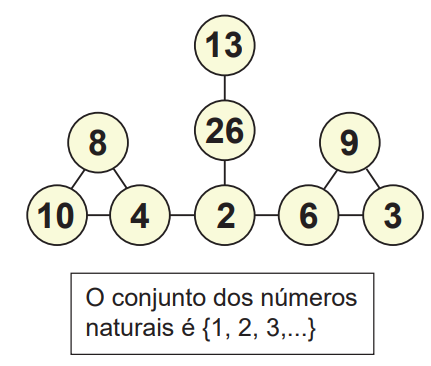
Questão 04. Os círculos do diagrama devem ser preenchidos com números naturais diferentes. Dois números escritos em círculos ligados por um segmento devem ter um divisor comum maior que 1.
Por exemplo, 8 e 15 nunca vão se ver em círculos ligados por um segmento. Abaixo temos um exemplo de preenchimento:
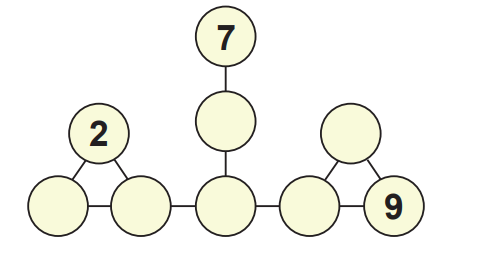
a) Faça um preenchimento para os círculos vazios abaixo.
b) Preencha os círculos de modo que o maior número escrito seja 12.
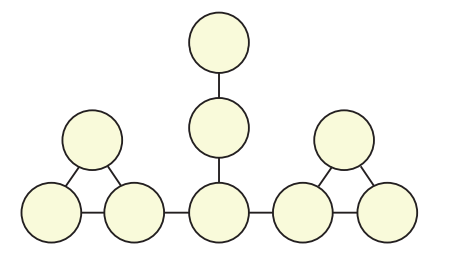
c) Explique por que é impossível preencher os círculos de modo que o maior número escrito seja menor do que 12.
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Os números precisam ter divisores comuns (maior que 1) quando estão conectados, e todos devem ser distintos. O desafio é preencher respeitando essa condição e minimizando o maior número usado, especialmente no item c).
1) Item a) – Preenchimento possível:

Um exemplo válido é:
7, 10, 70, 21, 6, 9
Todos os pares conectados têm um divisor comum maior que 1. Por exemplo:
- 10 e 70 têm divisor comum 10
- 70 e 21 têm divisor comum 7
- 6 e 9 têm divisor comum 3
✅ Conclusão do item a):
- O preenchimento respeita todas as condições de divisibilidade.
2) Item b) – Preenchimento com maior número igual a 12:

Exemplo de preenchimento:
5, 3, 6, 12, 9, 4, 8
Todos os pares conectados têm divisores comuns maiores que 1, e o maior número utilizado é 12.
✅ Conclusão do item b):
- O preenchimento é possível com o maior número sendo exatamente 12.
3) Item c) – Por que não é possível preencher com números menores que 12:
Se o maior número for menor que 12, os números disponíveis se restringem a 1 até 11. No entanto:
- O número 1 nunca pode ser usado (não tem divisor comum com nenhum outro além de 1).
- Números primos pequenos, como 7 e 11, não são bons candidatos pois seus múltiplos estão acima de 11.
- Com 8 círculos a preencher e restrições de ligação, é impossível selecionar 8 números distintos todos com divisores comuns com seus vizinhos.
Portanto, abaixo de 12 não é possível montar um diagrama completo e válido.
✅ Conclusão do item c):
- Não há como preencher os círculos de forma válida com todos os números menores que 12.
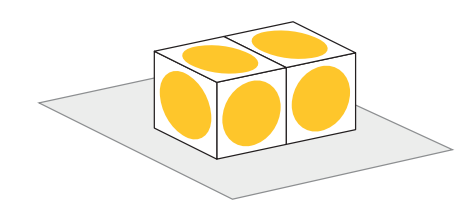
Questão 05. Janaína tem vários dados idênticos com faces numeradas de 1 a 6. Nesses dados, a soma dos números em faces opostas é sempre igual a 7. Ela cola alguns desses dados e coloca adesivos nas faces não coladas, inclusive nas faces que estão em contato com a mesa.
a) Qual é a menor soma possível para todos os números que foram cobertos por adesivos nos dois dados colados abaixo?
b) Janaína colou vários dados como mostrado abaixo. Quantos adesivos ela usou?
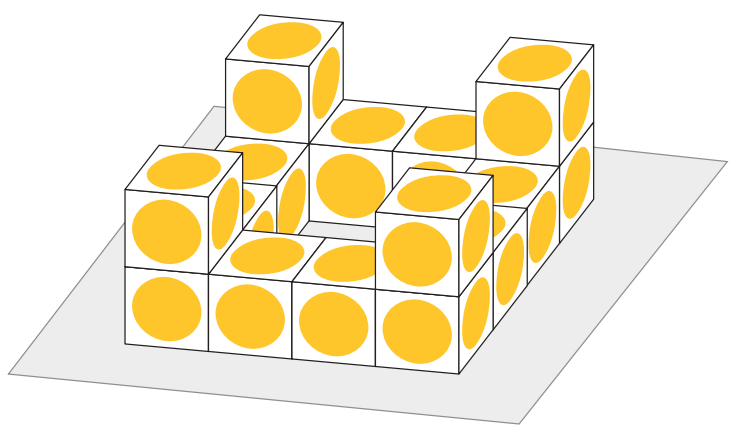
c) Na colagem de dados do item b), qual é a menor soma possível para todos os números que foram cobertos por adesivos?
🔍 Ver solução passo a passo
1) Item a – Menor soma possível dos números cobertos nos dois dados colados:
As faces de um dado somam: $$1 + 2 + 3 + 4 + 5 + 6 = 21$$
Em dois dados: $$2 \times 21 = 42$$
A menor soma possível para as faces cobertas por adesivos ocorre quando as faces coladas entre os dados são aquelas com os maiores números, ou seja, os números 6. Isso deixa os menores valores disponíveis para os adesivos.
Se duas faces coladas somam $$6 + 6 = 12$$, então os adesivos cobrem: $$42 – 12 = 30$$
✅ Conclusão do item a):
- Menor soma possível para os números cobertos por adesivos: $$30$$
2) Item b – Quantos adesivos foram usados?
Há 16 dados no total.
- 4 dados no topo → $$4 \times 5 = 20$$ faces adesivadas
- 4 dados abaixo do topo → $$4 \times 3 = 12$$ faces adesivadas
- 8 dados na base → $$8 \times 4 = 32$$ faces adesivadas
Total de adesivos:
$$20 + 12 + 32 = 64$$
✅ Conclusão do item b):
- Quantidade total de adesivos usados: $$64$$
3) Item c – Menor soma possível para os números cobertos por adesivos (caso b):
A menor soma ocorre quando as faces coladas são aquelas com os maiores valores, de forma que os adesivos cubram os menores.
- Faces adesivadas dos 4 dados do topo: $$4 \times (1 + 2 + 3 + 4 + 5) = 4 \times 15 = 60$$
- Faces adesivadas dos 4 dados abaixo: $$4 \times (1 + 2 + 3) = 12$$
- Faces adesivadas dos 8 dados na base: $$8 \times 7 = 56$$
Total:
$$60 + 12 + 56 = 128$$
✅ Conclusão do item c):
- Menor soma possível dos números cobertos por adesivos: $$128$$
Questão 06. Uma tabela 4×4, preenchida com os números 0 e 1, é equilibrada quando, somando os números em cada linha, obtemos todos os inteiros de 1 a 4, o mesmo ocorrendo com as somas dos números de cada coluna. Por exemplo, a tabela ao lado é equilibrada.
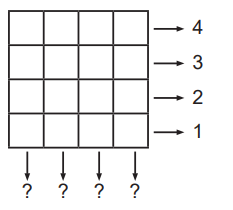
a)Preencha as tabelas abaixo de modo que elas sejam equilibradas, com as linhas e colunas tendo as somas indicadas.
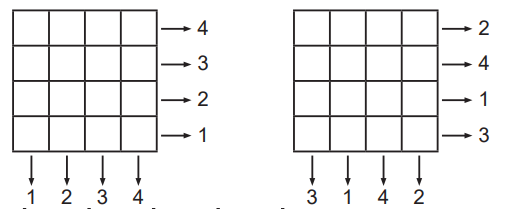
b) Quantas são as tabelas equilibradas com a soma de cada linha indicada abaixo?

c) Quantas são as tabelas equilibradas?
🔍 Ver solução passo a passo
Item a – Tabelas equilibradas com somas indicadas:
As tabelas podem ser preenchidas conforme o exemplo abaixo:
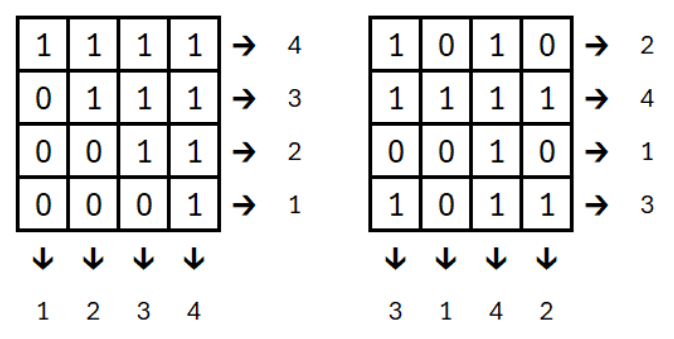
Cada tabela foi preenchida com 0 e 1 de forma que as somas das linhas e colunas correspondem exatamente aos números indicados.
Item b – Quantidade de tabelas equilibradas com linhas fixas:
Se fixarmos a soma das linhas como 4, 3, 2 e 1 (como no enunciado), a quantidade de tabelas depende da quantidade de maneiras de atribuir essas somas às colunas.
Há:
- 4 opções para a posição da soma 4
- 3 opções para a posição da soma 3
- 2 opções para a posição da soma 2
- 1 opção para a posição da soma 1
Logo:
$$ 4 \times 3 \times 2 \times 1 = 24 \text{ tabelas equilibradas} $$
✅ Conclusão do item b):
- Existem 24 tabelas equilibradas diferentes com as somas de linha fixas em 4, 3, 2 e 1.
Item c – Total de tabelas equilibradas:
Como as linhas podem estar em qualquer uma das 24 permutações possíveis e as colunas também, temos:
$$ 24 \times 24 = 576 \text{ tabelas equilibradas} $$
✅ Conclusão do item c):
- Há 576 tabelas equilibradas diferentes ao considerar todas as permutações possíveis das somas de linhas e colunas.
































