Enunciado:
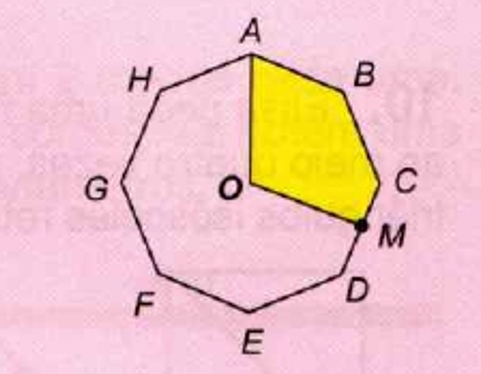
Na figura, ABCDEFGH é um octógono regular de centro O. O ponto M é o ponto médio do lado CD e a área do octógono é igual a 16 cm². Qual é a área da região amarela?
Imagem da questão:
Alternativas:
- (A) 5 cm²
- (B) 4,0 cm²
- (C) 4,5 cm²
- (D) 5,5 cm²
- (E) 6 cm²
Ver Solução
1. Divisão do octógono:
Como o octógono é regular e centrado em O, as diagonais partindo do centro o dividem em 8 triângulos isósceles congruentes.
Sendo a área total do octógono \(16\ \text{cm}^2\), cada um desses triângulos tem área:
\[ \frac{16}{8} = 2\ \text{cm}^2 \]
2. Identificação da região amarela:
A região amarela é formada pelos triângulos \( \triangle OAB \), \( \triangle OBC \), e metade do triângulo \( \triangle OCD \), pois \( M \) é o ponto médio de \( CD \).
Logo, temos:
- \( \triangle OAB = 2\ \text{cm}^2 \)
- \( \triangle OBC = 2\ \text{cm}^2 \)
- \( \triangle OMC = \frac{1}{2} \cdot 2 = 1\ \text{cm}^2 \)
3. Área total da região amarela:
\[ 2 + 2 + 1 = \boxed{5\ \text{cm}^2} \]
✅ Gabarito: Letra A
🧠 Mapas Mentais de Matemática























