Planificação do Paralelepípedo (rede): como montar e calcular áreas
Entenda a planificação do paralelepípedo (também chamada de rede ou net): como desenhar e recortar, onde ficam as medidas, e como obter a área total e a área lateral diretamente da planificação. Inclui exemplos com contas na vertical e exercícios.
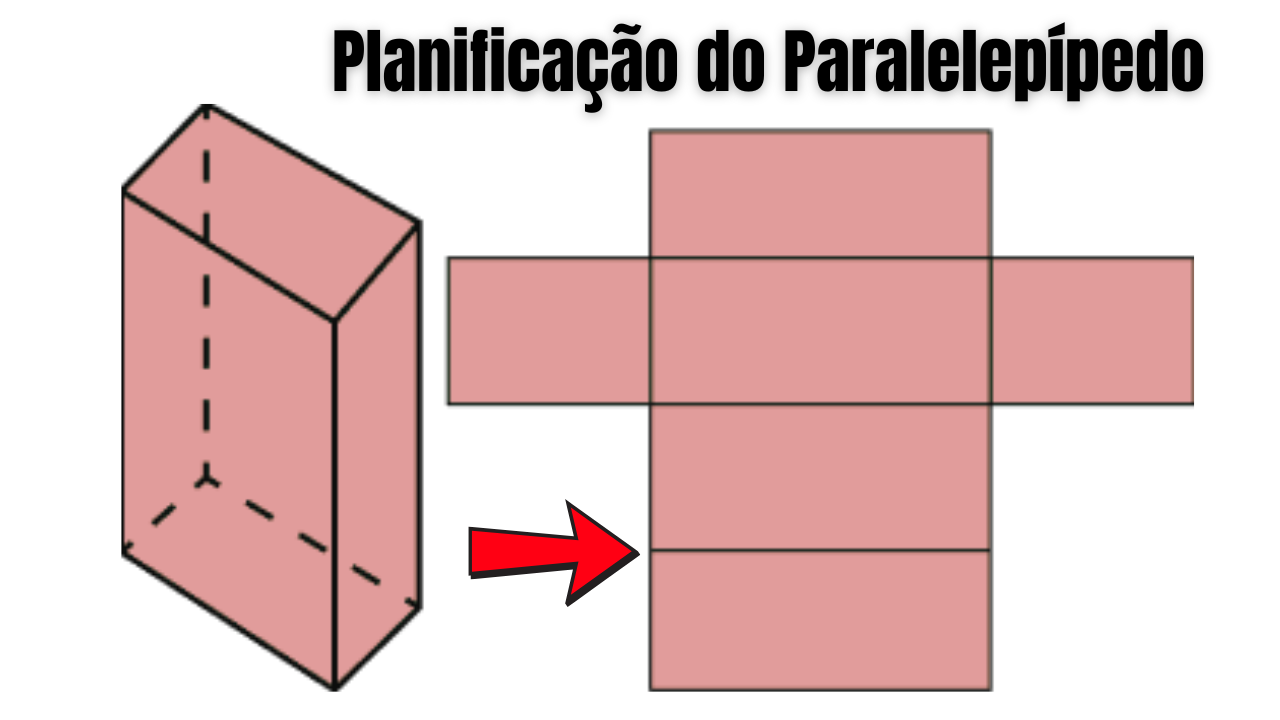
1) O que é a planificação do paralelepípedo?
É a representação, em uma única figura plana, de todas as faces do paralelepípedo, dispostas de modo que seja possível recortar e dobrar para reconstruir o sólido. No paralelepípedo retângulo com arestas \(a\), \(b\), \(c\), as faces são retângulos:
- 2 faces \(a\times b\) (bases opostas);
- 2 faces \(a\times c\);
- 2 faces \(b\times c\).
Existem várias planificações possíveis (diferentes “arranjos” dos 6 retângulos), mas todas têm as mesmas áreas somadas.
2) Como identificar medidas na rede
- Escolha um retângulo para ser a base (por ex., \(a\times b\)).
- As faces laterais adjacentes à base terão uma dimensão igual à altura \(c\).
- Os pares opostos são congruentes: meça uma face e “duplique” na soma da área.
3) Fórmulas obtidas a partir da planificação
Área total (retângulo)
\(A_t = 2(ab+ac+bc)\)
Soma das áreas dos 6 retângulos da rede.
Área lateral (base \(a\times b\))
\(A_l = 2c(a+b)\)
Corresponde às 4 faces “da volta”. Se a base for \(b\times c\), então \(A_l=2a(b+c)\); se for \(a\times c\), \(A_l=2b(a+c)\).
Perímetro útil da base (para a faixa lateral)
\(P_{\text{base}} = 2(a+b)\) → a “faixa” lateral tem área \(P_{\text{base}}\cdot c\). Em seguida, somam-se as duas bases \(2ab\) para obter \(A_t\).
4) Exemplos resolvidos (contas na vertical)
-
Enunciado. Um paralelepípedo retângulo tem \(a=8\ \text{cm}\), \(b=5\ \text{cm}\) e \(c=3\ \text{cm}\). Calcule a área total a partir da planificação.
Ver solução
$$\begin{aligned} A_t&=2(ab+ac+bc)\\ &=2(8\cdot5+8\cdot3+5\cdot3)\\ &=2(40+24+15)\\ &=2\cdot79\\ &=\mathbf{158\ \text{cm}^2} \end{aligned}$$ -
Enunciado. A planificação mostra uma faixa lateral contínua (perímetro da base) com comprimento \(2(a+b)\) e altura \(c=12\ \text{cm}\). Se \(a=10\ \text{cm}\) e \(b=6\ \text{cm}\), calcule a área lateral.
Ver solução
$$\begin{aligned} A_l&=2c(a+b)\\ &=2\cdot12\cdot(10+6)\\ &=24\cdot16\\ &=\mathbf{384\ \text{cm}^2} \end{aligned}$$ -
Enunciado. A rede tem duas bases \(a\times b\) com \(a=30\ \text{cm}\) e \(b=20\ \text{cm}\), e quatro retângulos laterais medindo \(c\times a\) e \(c\times b\) com \(c=50\ \text{cm}\). Encontre \(A_t\) e confirme que ela coincide com a soma das áreas dos 6 retângulos.
Ver solução
Pelo modelo \(A_t=2(ab+ac+bc)\):
$$\begin{aligned} A_t&=2(30\cdot20+30\cdot50+20\cdot50)\\ &=2(600+1500+1000)\\ &=2\cdot3100\\ &=\mathbf{6200\ \text{cm}^2} \end{aligned}$$Somando face a face na rede:
$$\begin{aligned} 2(ab)&=2\cdot(30\cdot20)=1200\\ 2(ac)&=2\cdot(30\cdot50)=3000\\ 2(bc)&=2\cdot(20\cdot50)=2000\\ \text{soma}&=1200+3000+2000=\mathbf{6200\ \text{cm}^2} \end{aligned}$$
Erros comuns ao trabalhar com a planificação
- Esquecer que existem duas bases: sempre some \(2ab\).
- Confundir área lateral com área total. A lateral não inclui as bases.
- Usar medidas em unidades diferentes (cm e m) sem padronizar.
- “Perder” um retângulo na rede por causa do arranjo escolhido: conte sempre 6 faces.
5) Exercícios (com solução em abre/fecha)
-
Na planificação de um paralelepípedo retângulo, as bases têm \(12\ \text{cm}\times 9\ \text{cm}\) e a altura é \(7\ \text{cm}\). Encontre \(A_l\) e \(A_t\).
Ver solução
$$\begin{aligned} A_l&=2c(a+b)\\ &=2\cdot7\cdot(12+9)\\ &=14\cdot21\\ &=294\ \text{cm}^2\\[6pt] A_t&=A_l+2ab\\ &=294+2(12\cdot9)\\ &=294+2\cdot108\\ &=294+216\\ &=\mathbf{510\ \text{cm}^2} \end{aligned}$$ -
Uma rede tem quatro retângulos \(c\times a\) e \(c\times b\) com \(c=15\ \text{cm}\), \(a=10\ \text{cm}\), \(b=6\ \text{cm}\). Qual é a área apenas da faixa lateral contínua?
Ver solução
$$\begin{aligned} A_{\text{faixa}}&=P_{\text{base}}\cdot c\\ &=2(a+b)\cdot c\\ &=2(10+6)\cdot15\\ &=32\cdot15\\ &=\mathbf{480\ \text{cm}^2} \end{aligned}$$ -
Sabendo que a área total da planificação é \(A_t=1{,}58\ \text{m}^2\) e que \(a=0{,}8\ \text{m}\), \(b=0{,}5\ \text{m}\), determine \(c\) (use \(A_t=2(ab+ac+bc)\)).
Ver solução
$$\begin{aligned} A_t&=2(ab+ac+bc)\\ 1{,}58&=2(0{,}8\cdot0{,}5+0{,}8\cdot c+0{,}5\cdot c)\\ 1{,}58&=2(0{,}40+1{,}3c)\\ 1{,}58&=0{,}80+2{,}6c\\ 2{,}6c&=1{,}58-0{,}80\\ 2{,}6c&=0{,}78\\ c&=\dfrac{0{,}78}{2{,}6}\\ c&=\mathbf{0{,}30\ \text{m}} \end{aligned}$$
6) Perguntas frequentes
| Quantas planificações diferentes existem? | Muitas: qualquer arranjo com 6 retângulos conectados que permita dobrar sem sobrepor já é uma planificação válida. |
|---|---|
| A planificação muda as fórmulas? | Não. A soma das áreas das 6 faces é sempre \(2(ab+ac+bc)\), independentemente do arranjo. |
| Como passar da planificação para a área lateral? | Some as quatro faces laterais. Para base \(a\times b\), \(A_l=2c(a+b)\). |






















