Planificação Prisma hexagonal

Planificação do Prisma hexagonal: como fazer, fórmulas e exemplos

Planificação do Prisma hexagonal

Veja como construir a rede (net) do prisma hexagonal, quais dimensões usar na faixa lateral, como calcular a área da chapa com ou sem aba, além de exemplos resolvidos e exercícios.

Planificação típica: faixa lateral com 6 retângulos + 2 hexágonos das bases.

1) O que é a planificação?

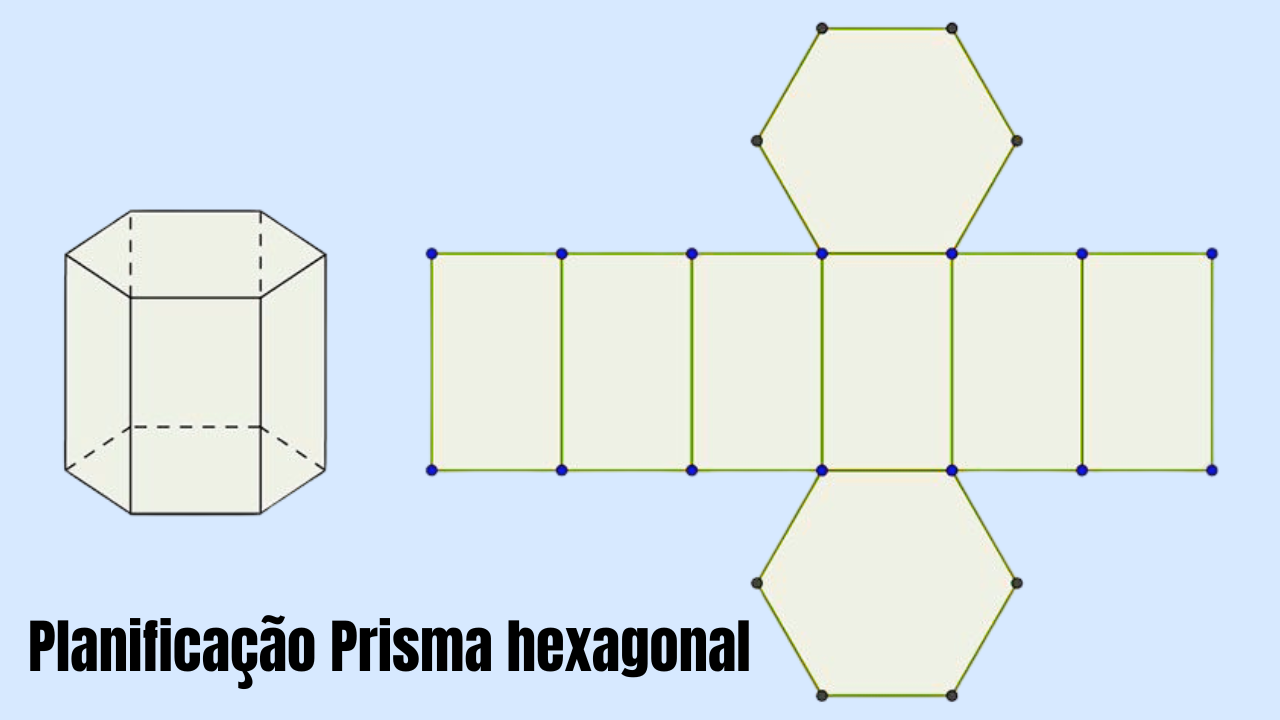
Planificar um sólido é “abrir” suas faces num único plano, obtendo um desenho que, ao ser recortado e dobrado, reconstrói o sólido original. Para o prisma hexagonal, a planificação é formada por:

uma faixa retangular de dimensões $p\times h$, subdividida em 6 retângulos (um para cada face lateral);
duas bases hexagonais congruentes.

Relembre a geometria do prisma na página Prismas regulares e a visão geral de poliedros.

2) Como construir a planificação

Desenhe a faixa lateral de largura $h$ (altura do prisma).
Defina o comprimento da faixa como o perímetro da base $p$. Para base regular (lado $a$), $p=6a$.
Divida a faixa em 6 retângulos, cada um com largura igual ao lado correspondente do hexágono.
Acople as duas bases: uma na “terceira” ou “quarta” face para facilitar a montagem, e a outra na face oposta.
Se for colar, acrescente uma aba de largura $w$ (geralmente 1 cm) ao longo de uma aresta lateral.

Para comparar, veja também a planificação do prisma pentagonal e a planificação do paralelepípedo.

3) Fórmulas úteis para a chapa

Faixa lateral: $A_L = p \cdot h$

Área total da planificação (sem abas): $A_{\text{chapa}} = p\cdot h + 2A_b$

Com uma aba de largura $w$ (ao longo da altura): $A_{\text{chapa+aba}} = p\cdot h + 2A_b + w\cdot h$

Base hexagonal regular (lado $a$)

Perímetro: $p=6a$

Área da base: $A_b=\dfrac{3\sqrt{3}}{2}\,a^2$

Para calcular $A_b$ por decomposição em triângulos, consulte Área de triângulo.

4) Exemplos resolvidos

Exemplo 1 — Área da planificação (sem abas)

Situação-problema. Deseja-se planificar um prisma hexagonal regular com lado $a=5\ \text{cm}$ e altura $h=12\ \text{cm}$. Calcule a área da chapa (faixa + 2 bases), sem abas.

Ver solução

$$\begin{aligned} p &= 6a\\ &= 6\cdot 5\\ &= 30\ \text{cm}\\[6pt] A_L &= p\cdot h\\ &= 30\cdot 12\\ &= 360\ \text{cm}^2\\[6pt] A_b &= \frac{3\sqrt{3}}{2}a^2\\ &= \frac{3\sqrt{3}}{2}\cdot 5^2\\ &= \frac{75\sqrt{3}}{2}\ \text{cm}^2\\[6pt] A_{\text{chapa}} &= A_L + 2A_b\\ &= 360 + 2\cdot \frac{75\sqrt{3}}{2}\\ &= 360 + 75\sqrt{3}\\ &\approx 360 + 129{,}90\\ &\approx \boxed{489{,}90\ \text{cm}^2} \end{aligned}$$

Exemplo 2 — Planificação com aba de 1 cm

Situação-problema. Para o mesmo prisma do Exemplo 1, será usada uma aba de largura $w=1\ \text{cm}$ ao longo de toda a altura. Qual a área total de papel?

Ver solução

$$\begin{aligned} A_{\text{chapa}} &= 360 + 75\sqrt{3}\\ &\approx 489{,}90\ \text{cm}^2\\[6pt] A_{\text{aba}} &= w\cdot h\\ &= 1\cdot 12\\ &= 12\ \text{cm}^2\\[6pt] A_{\text{total}} &= A_{\text{chapa}} + A_{\text{aba}}\\ &\approx 489{,}90 + 12\\ &\approx \boxed{501{,}90\ \text{cm}^2} \end{aligned}$$

Exemplo 3 — Custo da planificação

Situação-problema. Um totem em forma de prisma hexagonal regular tem $a=6\ \text{cm}$ e $h=20\ \text{cm}$. A planificação terá uma aba de $w=1\ \text{cm}$. O papel custa R$ 45,00/m². Qual o custo da chapa?

Ver solução

$$\begin{aligned} p &= 6a\\ &= 36\\[6pt] A_L &= p\cdot h\\ &= 36\cdot 20\\ &= 720\ \text{cm}^2\\[6pt] A_b &= \frac{3\sqrt{3}}{2}a^2\\ &= \frac{3\sqrt{3}}{2}\cdot 36\\ &= 54\sqrt{3}\ \text{cm}^2\\[6pt] A_{\text{chapa (sem abas)}} &= 720 + 2\cdot 54\sqrt{3}\\ &= 720 + 108\sqrt{3}\\ &\approx 720 + 187{,}06\\ &\approx 907{,}06\ \text{cm}^2\\[6pt] A_{\text{aba}} &= w\cdot h\\ &= 1\cdot 20\\ &= 20\ \text{cm}^2\\[6pt] A_{\text{total}} &\approx 907{,}06 + 20\\ &\approx 927{,}06\ \text{cm}^2\\[6pt] \text{em m}^2 &: \ 927{,}06\ \text{cm}^2 = 0{,}092706\ \text{m}^2\\[6pt] \text{Custo} &= 0{,}092706 \cdot 45\\ &\approx \boxed{\text{R\$ }4{,}17} \end{aligned}$$

5) Dicas para recorte e montagem

Vinco: trace levemente as linhas internas (sem cortar) para dobras limpas.
Posição das bases: fixe uma base no 3º ou 4º retângulo; a outra no retângulo oposto.
Aba: cole por dentro; 1 cm costuma ser suficiente.
Escala: ao ampliar em $k$, áreas multiplicam por $k^2$ e os comprimentos por $k$.

6) Exercícios propostos

(Regular) $a=4\ \text{cm}$, $h=15\ \text{cm}$. Calcule a área da planificação sem abas.
(Regular) $a=7\ \text{cm}$, $h=18\ \text{cm}$ e aba $w=1{,}5\ \text{cm}$. Calcule a área total da chapa.
(Custo) $a=5\ \text{cm}$, $h=20\ \text{cm}$, $w=1\ \text{cm}$; preço: R$ 52,00/m². Qual é o custo?
(Escala) Uma planificação calculada para $a=6\ \text{cm}$, $h=12\ \text{cm}$ foi ampliada em $k=1{,}3$. Por quanto multiplicar a área?
(Comparação) Para $a=5\ \text{cm}$, compare a largura total da faixa do prisma hexagonal com a do prisma pentagonal de mesmo lado e altura.

7) Continue estudando

Prismas regulares (guia) Prisma hexagonal — fundamentos e fórmulas Planificação do prisma pentagonal Poliedros Fórmula de Euler Sólidos de Platão Área de triângulo Paralelepípedo

8) Materiais do blog

🧠 Mapas Mentais de Matemática 🎯 ENEM Matemática 📚 Coleção 10 eBooks 🗃️ Banco de Questões de Matemática 📺 Canais Oficiais de Matemática

Relacionadas

Prisma hexagonal

Pirâmides

Sólidos de Platão

"Artigo escrito por"

Adriano Rocha

Sou Adriano Rocha, professor de Matemática com mestrado e especialização em Resolução de Problemas, além de expertise em concursos públicos. Leciono no Colégio Estadual Mimoso do Oeste e utilizo metodologias inovadoras para aprimorar a compreensão matemática e a resolução de problemas. Produzo conteúdos como artigos para blogs, livros, eBooks e mapas mentais, além de desenvolver materiais didáticos e participar de eventos acadêmicos, sempre com o objetivo de contribuir para o ensino e aprendizagem da Matemática.