Poliedros — definição, tipos (convexos e não convexos), fórmulas e exercícios
Tudo o que você precisa saber sobre poliedros: elementos, classificação, fórmula de Euler, sólidos de Platão, prismas e pirâmides, com exemplos e soluções em formato vertical.
1) O que é um poliedro?
Poliedro é um sólido geométrico limitado por polígonos planos (as faces). O encontro de duas faces forma uma aresta e o encontro de três ou mais faces forma um vértice.
Fórmula de Euler (poliedros convexos)
\( \boxed{V – E + F = 2} \) — relaciona número de vértices (V), arestas (E) e faces (F) em poliedros convexos (topologia de esfera).
2) Poliedros convexos × não convexos
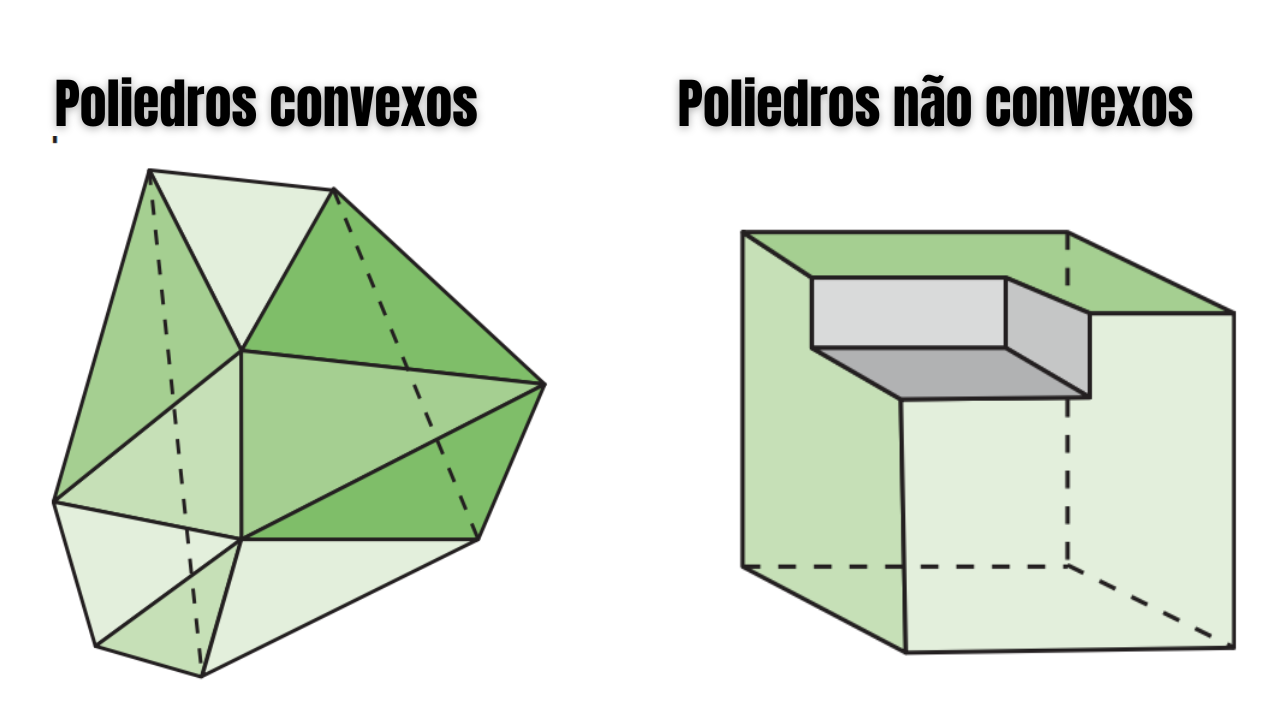
Definições rápidas
- Convexo: para quaisquer dois pontos do sólido, todo o segmento entre eles fica dentro do poliedro.
- Não convexo: possui reentrâncias (côncavo) ou auto-interseções (estrelado); algum segmento entre dois pontos sai do sólido.
Para não convexos sem auto-interseção mas ainda homeomorfos à esfera, Euler continua valendo; já para estrelados/“com furos”, a característica topológica muda.
3) Poliedros regulares (Sólidos de Platão)
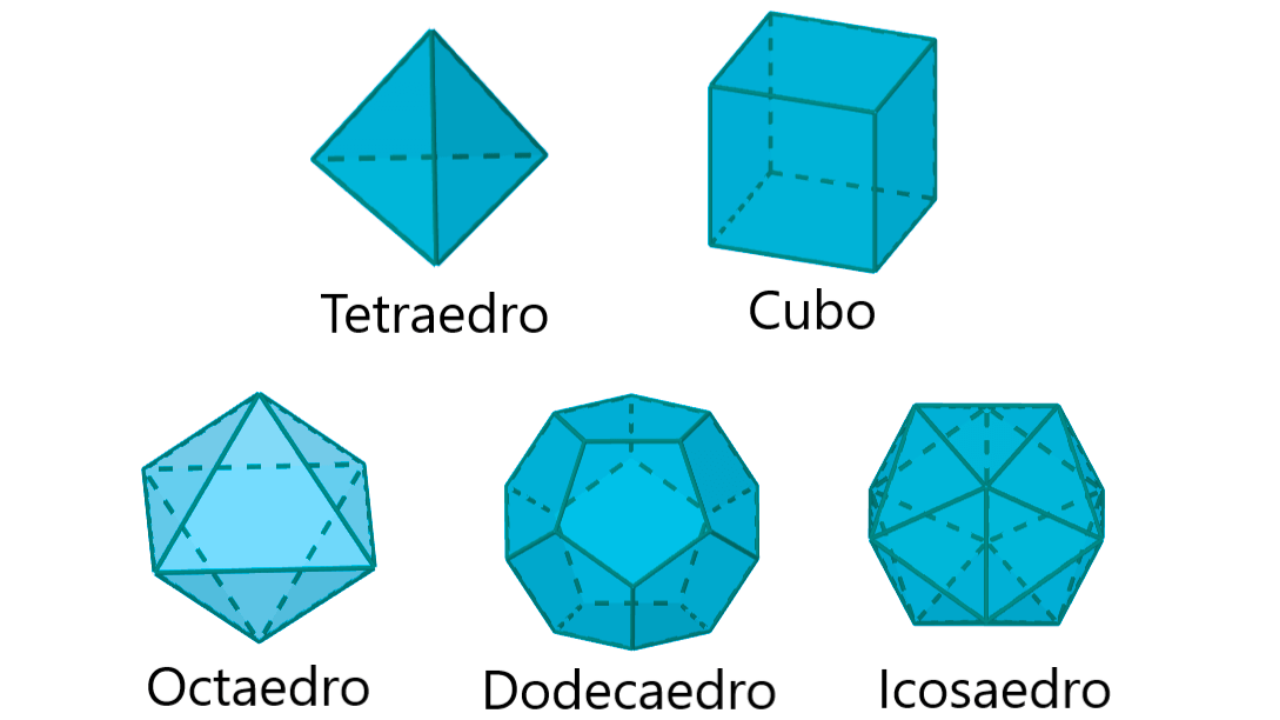
| Sólido | Faces | F | V | E | Dual |
|---|---|---|---|---|---|
| Tetraedro | Triângulos equiláteros | 4 | 4 | 6 | Tetraedro |
| Cubo (Hexaedro) | Quadrados | 6 | 8 | 12 | Octaedro |
| Octaedro | Triângulos equiláteros | 8 | 6 | 12 | Cubo |
| Dodecaedro | Pentágonos regulares | 12 | 20 | 30 | Icosaedro |
| Icosaedro | Triângulos equiláteros | 20 | 12 | 30 | Dodecaedro |
Dualidade: trocar faces por vértices preserva a contagem de arestas; ex.: cubo ↔ octaedro.
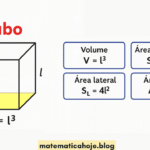
4) Prismas e pirâmides — fórmulas essenciais
Prismas
- Volume: \(V = A_{\text{base}}\cdot h\)
- Área lateral (prisma reto): \(A_l = P_{\text{base}}\cdot h\)
- Área total: \(A_t = A_l + 2A_{\text{base}}\)
Pirâmides
- Volume: \(V = \dfrac{A_{\text{base}}\cdot h}{3}\)
- Área total: \(A_t = A_{\text{base}} + A_{\text{lateral}}\) (soma dos triângulos laterais)
5) Planificação (rede)
A planificação é a figura plana formada por todas as faces de um poliedro, conectadas por arestas, de modo que se possa recortar e dobrar para reconstituir o sólido. Ela é excelente para calcular área total e para problemas de montagem.
Exemplo mental
Para um prisma retangular (paralelepípedo), a planificação tem 6 retângulos: \(2(ab), 2(ac), 2(bc)\). Assim, \(A_t=2(ab+ac+bc)\).
6) Exemplos resolvidos (contas na vertical)
-
Enunciado. Um prisma reto tem base um hexágono regular de lado \(a=4\ \text{cm}\). Sabendo que \(A_{\text{hex}}=\dfrac{3\sqrt{3}}{2}a^2\) e altura \(h=10\ \text{cm}\), calcule o volume.
Ver solução
$$\begin{aligned} A_{\text{base}}&=\frac{3\sqrt{3}}{2}\cdot 4^2\\ &=\frac{3\sqrt{3}}{2}\cdot16\\ &=24\sqrt{3}\ \text{cm}^2\\[4pt] V&=A_{\text{base}}\cdot h\\ &=24\sqrt{3}\cdot10\\ &=\mathbf{240\sqrt{3}\ \text{cm}^3} \end{aligned}$$ -
Enunciado. Uma pirâmide tem base quadrada de lado \(8\ \text{cm}\) e altura \(h=15\ \text{cm}\). Calcule o volume.
Ver solução
$$\begin{aligned} A_{\text{base}}&=8^2=64\\ V&=\frac{A_{\text{base}}\cdot h}{3}\\ &=\frac{64\cdot15}{3}\\ &=64\cdot5\\ &=\mathbf{320\ \text{cm}^3} \end{aligned}$$ -
Enunciado. Um poliedro convexo tem \(F=12\) faces pentagonais, \(V=20\) vértices. Calcule o número de arestas usando Euler.
Ver solução
$$\begin{aligned} V-E+F&=2\\ 20-E+12&=2\\ 32-E&=2\\ E&=32-2\\ E&=\mathbf{30} \end{aligned}$$Trata-se do dodecaedro: \(F=12, V=20, E=30\).
Erros comuns e como evitar
- Aplicar \(V-E+F=2\) em poliedros estrelados (auto-intersecção) sem ajustar a topologia.
- Confundir área lateral com área total em prismas/pirâmides.
- Não padronizar unidades antes de calcular (cm × m).
- Esquecer de considerar as duas bases na planificação de prismas.
7) Exercícios (com solução em abre/fecha)
-
Um prisma reto de base retângulo \(12\ \text{cm}\times 7\ \text{cm}\) e altura \(9\ \text{cm}\) deve ser embrulhado. Calcule a área total.
Ver solução
$$\begin{aligned} A_l&=P_{\text{base}}\cdot h=2(12+7)\cdot9=38\cdot9=342\\ A_t&=A_l+2A_{\text{base}}=342+2(12\cdot7)\\ &=342+2\cdot84\\ &=342+168\\ &=\mathbf{510\ \text{cm}^2} \end{aligned}$$ -
Uma pirâmide regular de base triangular equilátera \(a=10\ \text{cm}\) tem altura \(h=18\ \text{cm}\). Use \(A_{\triangle}=\dfrac{\sqrt{3}}{4}a^2\). Calcule o volume.
Ver solução
$$\begin{aligned} A_{\text{base}}&=\frac{\sqrt{3}}{4}\cdot10^2=25\sqrt{3}\\ V&=\frac{A_{\text{base}}\cdot h}{3}=\frac{25\sqrt{3}\cdot18}{3}\\ &=25\sqrt{3}\cdot6\\ &=\mathbf{150\sqrt{3}\ \text{cm}^3} \end{aligned}$$ -
Um poliedro (sem auto-interseção) possui \(F=10\), \(E=24\). Classifique a convexidade via Euler indicando \(V\).
Ver solução
$$\begin{aligned} V-E+F&=2\\ V-24+10&=2\\ V-14&=2\\ V&=16 \end{aligned}$$Como atende Euler com característica 2, pode ser convexo (ou ao menos homeomorfo à esfera).