Polígonos Semelhantes
Dois polígonos são semelhantes quando possuem os ângulos correspondentes iguais e os lados correspondentes proporcionais.
1) Definição de Polígonos Semelhantes
Dois polígonos são ditos semelhantes quando:
- Seus ângulos correspondentes são congruentes (iguais em medida);
- Os comprimentos de seus lados correspondentes são proporcionais.
Esse valor \(k\) é chamado de razão de semelhança.
2) Propriedades
- Ângulos correspondentes são iguais.
- Lados correspondentes são proporcionais.
- O perímetro dos polígonos semelhantes também é proporcional à razão de semelhança \(k\).
- As áreas dos polígonos semelhantes são proporcionais ao quadrado da razão de semelhança.
3) Exemplo
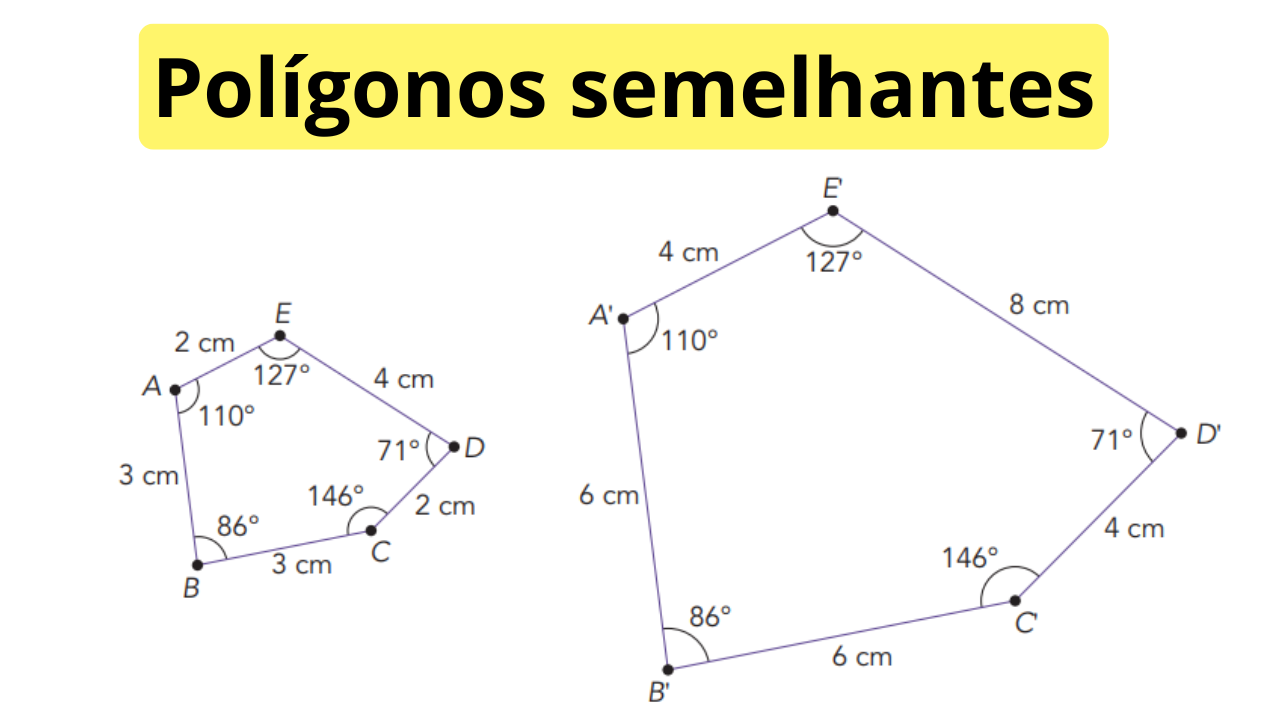
No diagrama acima, temos dois pentágonos semelhantes:
- Lados do polígono menor: 2 cm, 3 cm, 3 cm, 2 cm, 4 cm.
- Lados do polígono maior: 4 cm, 6 cm, 6 cm, 4 cm, 8 cm.
A razão de semelhança é \(k=\frac{4}{2}=2\). Todos os lados do polígono maior são o dobro dos lados correspondentes do polígono menor.
📘 Bloco de Exercícios – Polígonos Semelhantes
Resolva as questões abaixo:
1) Dois quadrados são semelhantes. O lado do maior mede 12 cm e o lado do menor 8 cm. A razão de semelhança é:
- 1,2
- 1,3
- 1,5
- 2
Ver solução
\(k=\frac{12}{8}=1,5\).
2) Dois triângulos semelhantes têm razão de semelhança \(k=3\). Se a área do menor é 10 cm², a área do maior é:
- 20 cm²
- 30 cm²
- 90 cm²
- 100 cm²
Ver solução
As áreas são proporcionais a \(k^2\). Logo: \(A_{maior}=10\cdot 3^2=90\).
3) Dois hexágonos semelhantes têm lados medindo 5 cm e 15 cm. A razão de semelhança é:
- 1/2
- 2
- 3
- 4
Ver solução
\(k=\frac{15}{5}=3\).
4) Dois retângulos semelhantes têm lados correspondentes de 6 cm e 9 cm no menor e 10 cm e \(x\) no maior. O valor de \(x\) é:
- 12
- 15
- 18
- 20
Ver solução
\(\dfrac{10}{6}=\dfrac{x}{9}\Rightarrow x=\frac{10\cdot9}{6}=15\).
5) O perímetro de um triângulo é 30 cm. Um triângulo semelhante a ele tem razão de semelhança 2. O perímetro do segundo triângulo é:
- 40 cm
- 60 cm
- 90 cm
- 120 cm
Ver solução
Perímetros são proporcionais a \(k\). Logo: \(30\cdot 2=60\).