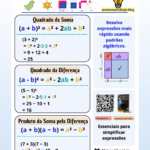
Quem estuda álgebra mais cedo ou mais tarde esbarra neles: os produtos notáveis. Eles aparecem em expressões, equações, funções, em questões do ENEM Matemática e em praticamente todos os concursos. O cartão de estudo mostrado na imagem abaixo resume, de forma visual, as fórmulas mais importantes: quadrado da soma, quadrado da diferença e produto da soma pela diferença.

Neste artigo, vou conduzir você passo a passo, como se estivéssemos em sala de aula, mostrando de onde vêm as fórmulas, como aplicá-las em situações de prova e como evitar os erros mais comuns. A ideia é que, ao final, você não apenas “decore”, mas entenda os produtos notáveis.
O que são produtos notáveis?
Em termos simples, produtos notáveis são multiplicações de expressões algébricas que aparecem com tanta frequência que vale a pena ter uma fórmula pronta para elas. Em vez de desenvolver tudo toda vez, você usa o padrão pronto e ganha tempo, especialmente em questões extensas do ENEM e de concursos.
A imagem destaca três protagonistas:
- Quadrado da soma: (a + b)²
- Quadrado da diferença: (a – b)²
- Produto da soma pela diferença: (a + b)(a – b)
Esses três casos já resolvem uma boa parte das expressões que aparecem em provas. Vamos olhar cada um com calma, sempre com exemplos numéricos para você sentir na prática.
Quadrado da soma: por que a fórmula funciona?
Comecemos pelo clássico quadrado da soma. A imagem traz a fórmula:
(a + b)2 = a2 + 2ab + b2
Mas de onde isso sai? Vamos desenvolver passo a passo. Lembre que “ao quadrado” significa multiplicar a expressão por ela mesma:
(a + b)2 = (a + b)(a + b)
Agora, aplicamos a distributiva (ou propriedade da soma no produto):
(a + b)(a + b) = a(a + b) + b(a + b)
= a·a + a·b + b·a + b·b
= a2 + ab + ab + b2
= a2 + 2ab + b2
Repare como a fórmula não apareceu do nada: é só o resultado de fazer distributiva com calma. Esse desenvolvimento é importante para você não ficar preso à decoração mecânica.
Agora, imagine uma situação de prova: o enunciado traz uma expressão como (x + 5)2 misturada em um cálculo de área, ou no desenvolvimento de uma função do segundo grau. Em vez de multiplicar tudo “na unha”, você faz:
(x + 5)2 = x2 + 2·x·5 + 52 = x2 + 10x + 25
Em muitos exercícios, depois de usar o produto notável, você ainda substitui um valor para x. Por exemplo, se o problema diz que x = 3:
(x + 5)2 = 32 + 10·3 + 25 = 9 + 30 + 25 = 64
Assim, você usa a fórmula e, ao mesmo tempo, treina a agilidade com contas, que é exatamente o que as provas cobram.
Quadrado da diferença: atenção ao sinal!
O segundo destaque da imagem é o quadrado da diferença:
(a − b)2 = a2 − 2ab + b2
A estrutura é parecida com a do quadrado da soma, mas o termo do meio vem com sinal negativo. Esse detalhe derruba muita gente em prova.
Se você desenvolver do zero, verá que:
(a − b)2 = (a − b)(a − b)
= a(a − b) − b(a − b)
= a·a − a·b − b·a + b·b
= a2 − ab − ab + b2
= a2 − 2ab + b2
Em aplicação prática, um exercício pode pedir, por exemplo, que você simplifique a expressão (2x − 3)2 antes de substituir um valor.
(2x − 3)2 = (2x)2 − 2·(2x)·3 + 32
= 4x2 − 12x + 9
Muitas questões de função quadrática, inequações e até problemas de geometria analítica usam esse tipo de expressão para modelar distância, área ou variação de grandezas. Reconhecer que se trata de um produto notável torna o cálculo mais rápido e limpo.
Produto da soma pela diferença: diferença de quadrados
A terceira fórmula mostrada na imagem é o produto da soma pela diferença:
(a + b)(a − b) = a2 − b2
Esse é conhecido como diferença de quadrados. Ele é muito útil na fatoração, na simplificação de frações algébricas e em várias questões de nível médio e de concursos.
Vamos desenvolver para entender o porquê:
(a + b)(a − b) = a(a − b) + b(a − b)
= a·a − a·b + b·a − b·b
= a2 − ab + ab − b2
= a2 − b2
No dia a dia de provas, você encontra expressões como (x + 4)(x − 4). Em vez de usar a distributiva dois a dois, já pode ir direto:
(x + 4)(x − 4) = x2 − 42 = x2 − 16
Em problemas práticos, esse tipo de produto aparece quando o enunciado fala em diferença de áreas, diferença de quadrados de medidas ou quando você precisa simplificar uma expressão antes de substituir valores numéricos.
Um exemplo típico: em uma questão de física, a energia cinética pode envolver a diferença entre o quadrado de duas velocidades. Reconhecer um padrão do tipo v22 − v12 como (v2 + v1)(v2 − v1) ajuda a manipular a equação com mais facilidade.
Conectando produtos notáveis a problemas reais de prova
Até aqui vimos as fórmulas e alguns exemplos diretos, mas os produtos notáveis ganham vida mesmo quando aparecem “escondidos” dentro de problemas. Imagine um enunciado que diz:
“A expressão que representa a área de um quadrado de lado (x + 3) metros é igual à de um retângulo de lados (x + 5) e (x − 5). Determine x.”
A área do quadrado é:
Aq = (x + 3)2
A área do retângulo é:
Ar = (x + 5)(x − 5)
Como o problema diz que as áreas são iguais, temos:
(x + 3)2 = (x + 5)(x − 5)
Agora é a hora de usar o que aprendemos:
(x + 3)2 = x2 + 6x + 9
(x + 5)(x − 5) = x2 − 25
x2 + 6x + 9 = x2 − 25
Cancelamos o x2 dos dois lados e ficamos com uma equação de primeiro grau:
6x + 9 = −25
6x = −34
x = −34/6 = −17/3
Perceba a cadeia de ideias: área → expressão algébrica → produto notável → equação. Exatamente o tipo de raciocínio que bancos de prova adoram cobrar.
Para quem está se preparando com mais profundidade, vale buscar listas específicas de questões que exploram produtos notáveis, tanto no pacote de 10 eBooks de Matemática quanto em materiais focados em treino de questões, como o Banco de Questões de Matemática .
Como fixar produtos notáveis sem decorar “no vazio”
Uma das melhores maneiras de fixar produtos notáveis é misturá-los com outros conteúdos: função do segundo grau, equações, problemas geométricos, porcentagem e até progressões. Sempre que vir algo ao quadrado ou um produto que lembra soma pela diferença, pergunte a si mesmo: “Isso é um produto notável disfarçado?”
Outra estratégia é montar um pequeno roteiro de estudo: primeiro, rever as fórmulas em um resumo bem organizado; depois, resolver alguns exemplos simples; por fim, encarar questões de ENEM e concursos que misturam vários assuntos. Assim, você cria o hábito de reconhecer os padrões na prática.
Se você gosta de ter um caminho mais estruturado para o ENEM, vale também organizar seus estudos por eixo, revendo álgebra, funções, geometria e estatística de forma integrada. O material do ENEM Matemática ajuda bastante nessa organização, especialmente para quem está retomando os estudos ou quer subir a nota na próxima prova.