Dois móveis partem do mesmo ponto e descrevem trajetórias retilíneas e perpendiculares entre si. Os móveis possuem velocidades constantes \(V\) e \(2V\), respectivamente. Após um tempo \(t\), a distância entre os móveis é igual a \(x\). A partir daí, passados mais \(3t\), a distância entre os móveis será:
(A) \(2x\)
(B) \(3x\)
(C) \(4x\)
(D) \(5x\)
(E) \(6x\)
Ver solução passo a passo
Resposta correta: (C)
Como a velocidade de um móvel é o dobro do outro, em qualquer instante \(t\) a distância percorrida pelo móvel mais rápido é o dobro da distância percorrida pelo mais lento.
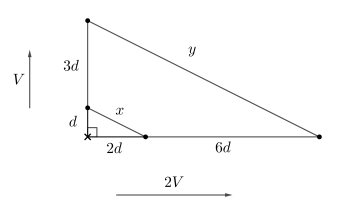
Após o tempo \(t\): \[ \text{Distância horizontal} = 2Vt, \quad \text{Distância vertical} = Vt \] \[ x = \sqrt{(2Vt)^2 + (Vt)^2} = \sqrt{5}Vt \]
Após mais \(3t\), os deslocamentos serão: \[ \text{Horizontal} = 8Vt, \quad \text{Vertical} = 4Vt \] A distância \(y\) entre os móveis será: \[ y = \sqrt{(8Vt)^2 + (4Vt)^2} = \sqrt{80V^2t^2} = 4\sqrt{5}Vt \]
Como \(x = \sqrt{5}Vt\), temos: \[ y = 4x \]
📘 E baixe os 10 eBooks de Matemática para turbinar seus estudos!
































