Michel tem à sua disposição 3 pizzas quadradas, com medidas diferentes, mas todas de mesma espessura. Ele pode escolher entre comer apenas as duas pizzas menores ou apenas a maior. Desejando comer o máximo possível de pizza, Michel organizou as pizzas como mostra a figura.
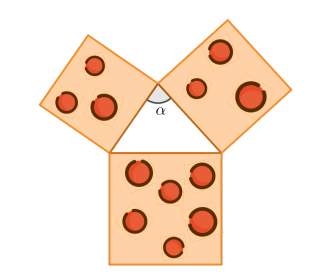
Para ser vantajoso para Michel comer as duas pizzas menores, é necessário e suficiente que:
(B) \( \alpha \) seja um ângulo reto.
(C) \( \alpha \) seja um ângulo obtuso.
(D) \( \alpha > 60^\circ \).
(E) \( \alpha < 60^\circ \).
Resposta correta: (A) \( \alpha \) é um ângulo agudo.
Vamos chamar:
- \( d \) → lado da pizza maior
- \( b \) → lado da segunda pizza
- \( c \) → lado da menor pizza
Pela Lei dos Cossenos, temos:
\[ d^2 = b^2 + c^2 – 2bc \cdot \cos(\alpha) \]
Sabemos que \( d^2 \) é a área da pizza maior (\( A_1 \)) e \( b^2 + c^2 \) é a soma das áreas das pizzas menores (\( A_2 \)):
\[ A_1 = A_2 – 2bc\cos(\alpha) \]
Para que seja vantajoso comer as duas pizzas menores:
\[ A_2 > A_1 \quad \Rightarrow \quad A_2 > A_2 – 2bc\cos(\alpha) \quad \Rightarrow \quad \cos(\alpha) > 0 \]
Logo, \( 0^\circ < \alpha < 90^\circ \), ou seja, \( \alpha \) é um ângulo agudo.
🔗 Continue seus estudos com nossos recursos: