Propriedades da Função Logarítmica

Veja também: Função logarítmica (definição e gráfico) • Função exponencial (inversa) • Propriedades dos logaritmos • Logaritmo natural (ln) • Mudança de base • Equações logarítmicas

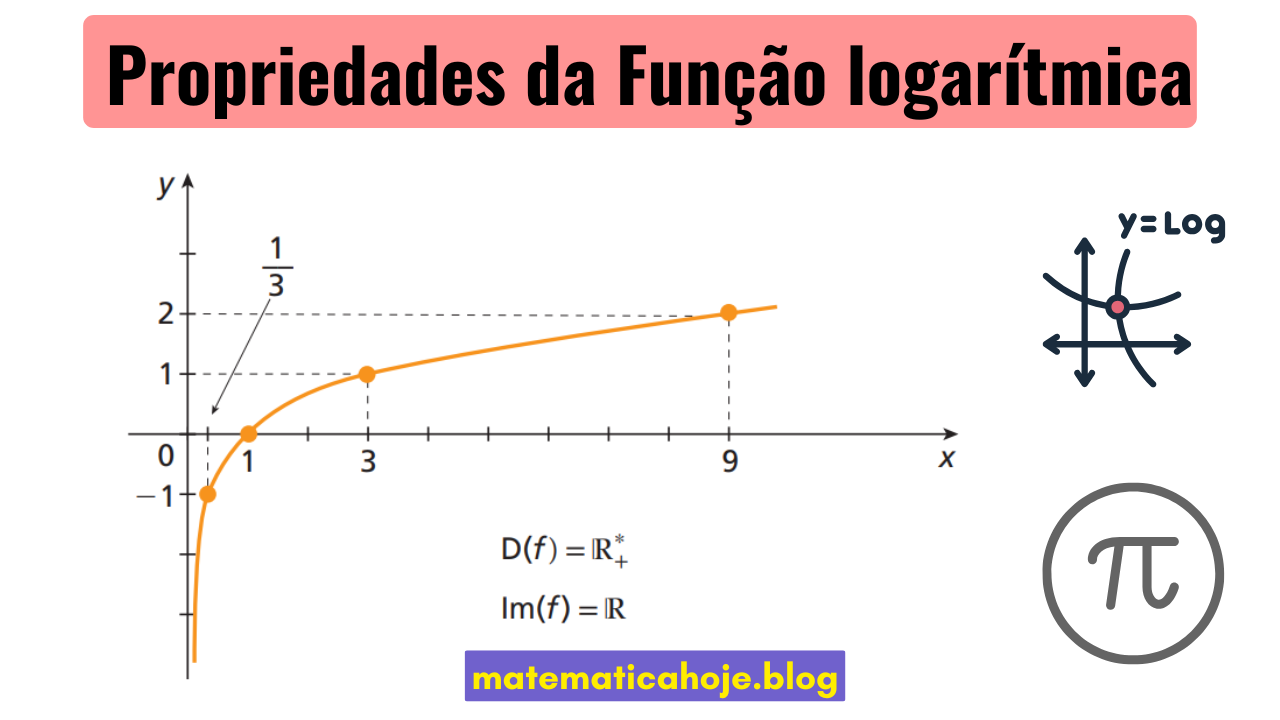
Para uma base \(a\) com \(a>0\) e \(a\neq 1\), a função logarítmica é \( f(x)=\log_a x \) com domínio \( (0,\infty) \). Abaixo, resumimos suas propriedades essenciais para resolver questões de vestibulares, ENEM e concursos.

Resumo das propriedades

Domínio \( D(f)=(0,\infty) \) — exige \( x>0 \).

Imagem \( \operatorname{Im}(f)=\mathbb{R} \).

Interseção Corta o eixo \(x\) em \( (1,0) \) pois \( \log_a 1=0 \).

Assíntota \( x=0 \) é assíntota vertical.

Crescimento Crescente se \( a>1 \); decrescente se 0 < a < 1.

Concavidade Concavidade voltada para baixo (é côncava).

Inversa Inversa de \( g(x)=a^{x} \); assim, \( g(f(x))=x \) e \( f(g(x))=x \).

Mudança de base \( \log_a x=\dfrac{\ln x}{\ln a} \) (relação com \( \ln \)).

Pontos notáveis do gráfico

\( (1,0) \) — sempre presente;
\( (a,1) \) — pois \( \log_a a=1 \);
\( (a^k,k) \) — em geral, \( \log_a(a^k)=k \) (útil para rascunho do gráfico).

Transformações

Para \( y = b\cdot \log_a(k(x-h)) + d \):

Domínio: \( k(x-h)>0 \).
Translada \(h\) à direita (se \(h>0\)) e \(d\) para cima.
Escalas: \(b\) (vertical) e \(1/k\) (horizontal).

\( \displaystyle \log_a(xy)=\log_a x+\log_a y,\quad \log_a\!\left(\frac{x}{y}\right)=\log_a x-\log_a y,\quad \log_a(x^r)=r\log_a x. \)

📘 eBook de Fórmulas Matemáticas — todas as propriedades de logaritmos e gráficos em um só lugar

Exemplos resolvidos

Exemplo 1 — Determine o domínio de \( f(x)=\log_3(2x-5) \).

Exige \( 2x-5>0 \Rightarrow x>\tfrac{5}{2} \). Logo, \( D(f)=\left(\tfrac{5}{2},\infty\right) \).

Exemplo 2 — A função \( g(x)=\log_{1/3}(x+1) \) é crescente ou decrescente?

Como 0 < a < 1 (aqui \( a=\tfrac{1}{3} \)), a função logarítmica é decrescente. Além disso, o domínio exige \( x+1>0 \Rightarrow x>-1 \).

Exemplo 3 — Resolva \( \log_2(x-3)\ge 1 \).

Condição de existência: \( x-3>0 \Rightarrow x>3 \). Como \( a=2>1 \), a desigualdade mantém o sentido ao “deslogaritmar”: \( x-3\ge 2^1=2 \Rightarrow x\ge 5 \). Solução: \( [5,\infty) \).

Exercícios de múltipla escolha

1) A assíntota vertical de \( y=\log_a x \) é:

a) \( y=0 \)
b) \( x=0 \)
c) \( x=1 \)
d) \( y=1 \)

Ver solução

Reta \( x=0 \). Alternativa b.

2) Para \( a>1 \), a função \( f(x)=\log_a x \):

a) é par
b) é ímpar
c) é crescente
d) é decrescente

Ver solução

Crescente. Alternativa c.

3) O ponto comum a todo gráfico de \( y=\log_a x \) é:

a) \( (0,1) \)
b) \( (1,0) \)
c) \( (a,0) \)
d) \( (0,a) \)

Ver solução

Ponto \( (1,0) \). Alternativa b.

4) O domínio de \( y=\log_4(5-2x) \) é:

a) \( x<\tfrac{5}{2} \)
b) \( x\le \tfrac{5}{2} \)
c) \( x> \tfrac{5}{2} \)
d) \( x\in\mathbb{R} \)

Ver solução

Exige \( 5-2x>0 \Rightarrow x<\tfrac{5}{2} \). Alternativa a.

5) Se \( y=\log_{1/2} x \), então:

a) \( y \) é crescente e \( D=(0,\infty) \)
b) \( y \) é decrescente e \( D=(0,\infty) \)
c) \( y \) é crescente e \( D=\mathbb{R} \)
d) \( y \) é decrescente e \( D=\mathbb{R} \)

Ver solução

Para 0 < a < 1 a função é decrescente e o domínio continua sendo \( (0,\infty) \). Alternativa b.

Leituras internas recomendadas (SEO)

Materiais e produtos do blog

Mapas mentais de Matemática — revisão visual por tema.
ENEM Matemática — teoria objetiva + questões.
Pacote com 10 eBooks — conteúdo para o ano inteiro.
Banco de questões — pratique por assunto e nível.
eBook de Fórmulas Matemáticas — todas as fórmulas de logaritmos, gráficos e dicas de rapidez.