Questão 6. (AFA-SP) A função real \( f \) definida por
$$ f(x) = a \cdot 3^x + b $$
com \( a \) e \( b \) constantes reais, está graficamente representada abaixo:
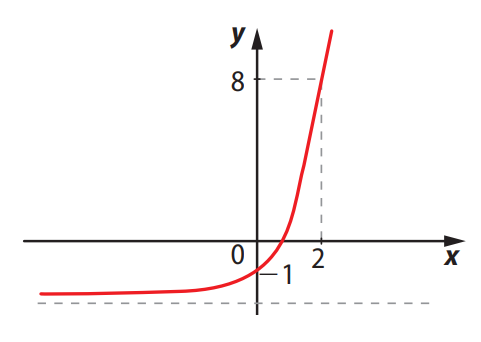
Pode-se afirmar que o produto \( a \cdot b \) pertence ao intervalo real:
- a) \( [-4, -1[ \)
- b) \( [-1, 2[ \)
- c) \( [2, 5[ \)
- d) \( [5, 8] \)
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
A função é \( f(x) = a \cdot 3^x + b \), e o gráfico mostra que:
- \( f(0) = -1 \)
- \( f(2) = 8 \)
1) Substituir \( x = 0 \) na função:
$$ f(0) = a \cdot 3^0 + b = a + b = -1 \quad \text{(Equação 1)} $$
2) Substituir \( x = 2 \):
$$ f(2) = a \cdot 3^2 + b = 9a + b = 8 \quad \text{(Equação 2)} $$
3) Resolver o sistema de equações:
Equação 1: \( a + b = -1 \)
Equação 2: \( 9a + b = 8 \)
Subtraindo a Equação 1 da Equação 2:
$$ (9a + b) – (a + b) = 8 – (-1) $$
$$ 8a = 9 \Rightarrow a = \frac{9}{8} $$
Substituindo em \( a + b = -1 \):
$$ \frac{9}{8} + b = -1 \Rightarrow b = -1 – \frac{9}{8} = -\frac{17}{8} $$
4) Calcular \( a \cdot b \):
$$ a \cdot b = \frac{9}{8} \cdot \left( -\frac{17}{8} \right) = -\frac{153}{64} \approx -2,39 $$
5) Verificar o intervalo que contém \( -2{,}39 \):
A única alternativa que contém esse valor é:
Alternativa a) \( [-4, -1[ \)
✅ Conclusão:
- Produto: \( a \cdot b \approx -2{,}39 \)
- Intervalo correto: \( [-4, -1[ \)













