Regra da Cadeia — Guia Completo
A Regra da Cadeia é essencial para derivar funções compostas. Revise também: definição de derivada, regras de derivação, produto e quociente, exponenciais, logarítmicas e trigonométricas.
1) Enunciado e intuição
Se \(h(x)=f(g(x))\) e \(f,g\) são deriváveis, então:
\(\displaystyle h'(x)=f’\big(g(x)\big)\cdot g'(x)\)
Intuição: derivada da função de fora (avaliada no resultado da de dentro) vezes a derivada da função de dentro.
Notação de Leibniz
Se \(y=f(u)\) e \(u=g(x)\), então
\(\displaystyle \frac{dy}{dx}=\frac{dy}{du}\cdot\frac{du}{dx}\)
2) Fórmulas úteis da Regra da Cadeia
Funções trigonométricas
Funções exponenciais
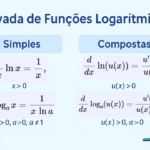
Funções logarítmicas
Funções trigonométricas inversas
3) Exemplos resolvidos
Exemplo 1 — \(\;h(x)=\sin(2x+1)\)
Mostrar solução
\(f'(u)=\cos u\), \(u’=2\).
\(\displaystyle h'(x)=2\cos(2x+1)\).
Exemplo 2 — \(\;h(x)=\sqrt{x^2+2x}\)
Mostrar solução
\(f'(u)=\dfrac{1}{2\sqrt{u}}\), \(u’=2x+2\).
\(\displaystyle h'(x)=\dfrac{x+1}{\sqrt{x^2+2x}}\).
Exemplo 3 — \(\;y=e^{\sin x}\)
Mostrar solução
\(f'(u)=e^u\), \(u’=\cos x\).
\(\displaystyle y’=e^{\sin x}\cos x\).
Exemplo 4 — \(\;w=\ln(t^4+2)\)
Mostrar solução
\(f'(u)=1/u\), \(u’=4t^3\).
\(\displaystyle w’=\dfrac{4t^3}{t^4+2}\).
4) Exercícios
- \(y=\sin(5x-3)\)
- \(f(x)=\cos(x^3)\)
- \(h(x)=\ln(2x^2+1)\)
- \(g(x)=e^{\tan x}\)
- \(p(x)=[4x-1]^7\)
- \(q(x)=\sqrt{3x^2-2x+5}\)
- \(r(x)=(1-x^2)^{-1/2}\)
- \(s(x)=\arctan(e^{x})\)
- \(w(t)=\ln(\cos 2t)\) (domínio: \(\cos 2t>0\))
- \(F(x)=e^{\sin(x^2)}\)
Mostrar gabarito
1) \(y’=5\cos(5x-3)\).
2) \(f'(x)=-3x^2\sin(x^3)\).
3) \(h'(x)=\dfrac{4x}{2x^2+1}\).
4) \(g'(x)=e^{\tan x}\sec^2x\).
5) \(p'(x)=28(4x-1)^6\).
6) \(q'(x)=\dfrac{6x-2}{2\sqrt{3x^2-2x+5}}\).
7) \(r'(x)=\dfrac{x}{(1-x^2)^{3/2}}\).
8) \(s'(x)=\dfrac{e^x}{1+e^{2x}}\).
9) \(w'(t)=-2\tan(2t)\).
10) \(F'(x)=2x\,e^{\sin(x^2)}\cos(x^2)\).
5) Leituras recomendadas
Lista de Exercícios — Regra da Cadeia
Exercícios detalhados com soluções passo a passo e observações importantes sobre domínios.
-
\(y=(3x^2+1)^5\)
Mostrar solução
Defina \(u=3x^2+1\).
\(\dfrac{dy}{dx}=5u^{4}\cdot u’\).
\(u’=6x\).
\(\boxed{\,y’=30x(3x^2+1)^4\,}\).
Observação: Domínio: \(\mathbb{R}\). -
\(f(x)=\sqrt{5x+7}\)
Mostrar solução
\(f(x)=(5x+7)^{1/2}\).
\(f'(x)=\tfrac12(5x+7)^{-1/2}\cdot 5\).
\(\boxed{\,f'(x)=\dfrac{5}{2\sqrt{5x+7}}\,}\).
Observação: Domínio: \(5x+7>0 \;\Rightarrow\; x>-\tfrac75\). -
\(h(x)=e^{2x+3}\)
Mostrar solução
\(h'(x)=e^{2x+3}\cdot 2\).
\(\boxed{\,h'(x)=2e^{2x+3}\,}\).
Observação: Domínio: \(\mathbb{R}\). -
\(g(x)=\ln(4x^2+1)\)
Mostrar solução
\(g'(x)=\dfrac{1}{4x^2+1}\cdot 8x\).
\(\boxed{\,g'(x)=\dfrac{8x}{4x^2+1}\,}\).
Observação: Argumento do log sempre positivo → domínio \(\mathbb{R}\). -
\(p(x)=\cos(7x-5)\)
Mostrar solução
\(p'(x)=-\sin(7x-5)\cdot 7\).
\(\boxed{\,p'(x)=-7\sin(7x-5)\,}\).
Observação: Domínio: \(\mathbb{R}\).
-
\(y=e^{\sin(3x)}\)
Mostrar solução
\(u=\sin(3x)\Rightarrow u’=\cos(3x)\cdot3\).
\(y’=e^u\cdot u’\).
\(\boxed{\,y’=3e^{\sin(3x)}\cos(3x)\,}\).
Observação: Domínio: \(\mathbb{R}\). -
\(f(x)=\ln(\sqrt{x^2+2x+5})\)
Mostrar solução
\(f(x)=\tfrac12\ln(x^2+2x+5)\).
\(f'(x)=\tfrac12\cdot\dfrac{2x+2}{x^2+2x+5}\).
\(\boxed{\,f'(x)=\dfrac{x+1}{x^2+2x+5}\,}\).
Observação: Argumento da raiz sempre positivo → domínio \(\mathbb{R}\). -
\(h(x)=\tan(2x^3-x)\)
Mostrar solução
\([\tan u]’=\sec^2u\cdot u’\).
\(u=2x^3-x\Rightarrow u’=6x^2-1\).
\(\boxed{\,h'(x)=(6x^2-1)\sec^2(2x^3-x)\,}\).
Observação: Domínio: onde \(\cos(2x^3-x)\neq0\). -
\(g(x)=\arcsin\left(\dfrac{x}{2}\right)\)
Mostrar solução
\([\arcsin u]’=\dfrac{u’}{\sqrt{1-u^2}}\).
\(u=\tfrac{x}{2}\Rightarrow u’=\tfrac12\).
\(\boxed{\,g'(x)=\dfrac{1}{\sqrt{4-x^2}}\,}\).
Observação: Domínio: \(|x|\le2\). -
\(p(x)=\sec(5x^2+1)\)
Mostrar solução
\([\sec u]’=\sec u\tan u\cdot u’\).
\(u=5x^2+1\Rightarrow u’=10x\).
\(\boxed{\,p'(x)=10x\,\sec(5x^2+1)\tan(5x^2+1)\,}\).
Observação: Domínio: onde \(\cos(5x^2+1)\neq0\).