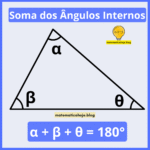
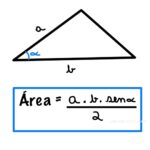
Relação entre Lados e Ângulos do Triângulo — lado maior ⇔ ângulo oposto maior

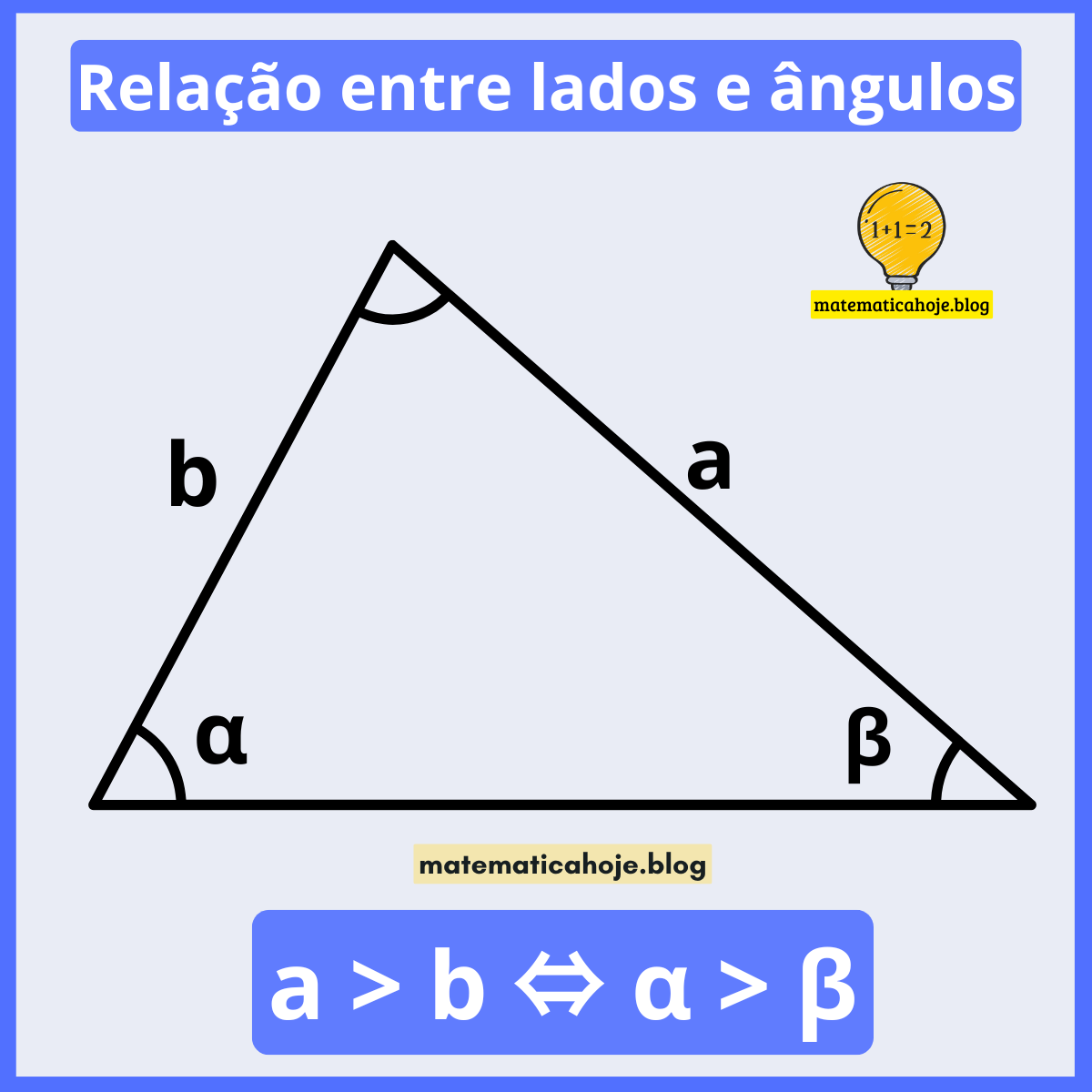
Em qualquer triângulo, se \(a > b\) então o ângulo oposto a \(a\) é maior que o ângulo oposto a \(b\): \( \alpha > \beta \). E o recíproco também é verdadeiro.

Regra central: \(a > b \;\Longleftrightarrow\; \alpha > \beta\) (ângulos opostos).

Essa relação decorre, por exemplo, da Lei dos Senos \( \frac{a}{\sin \alpha}=\frac{b}{\sin \beta}=\frac{c}{\sin \gamma} \): como o seno cresce em \( (0^\circ,180^\circ) \) para ângulos internos de triângulo, lados e ângulos opostos variam juntos.

Conecte este estudo com: Soma dos Ângulos Internos, Soma dos Ângulos Externos e o Teorema do Ângulo Externo.

Relação entre lados e ângulos: a > b ⇔ α > β — Imagem: matematicaoje.blog — maior lado ↔ maior ângulo oposto.

Intuição geométrica rápida

Mantendo dois lados fixos, abrir mais o vértice oposto “puxa” o terceiro lado, tornando-o maior. Inversamente, se um lado cresce, o ângulo à sua frente precisa abrir para “alcançar” os outros vértices.

Ângulos opostos Lei dos Senos Comparação de medidas

Mapas Mentais de Matemática — Destaque

Revisão visual de triângulos, ângulos, semelhança e também matemática básica (operações com números inteiros, regras de sinais, adição e subtração de inteiros, multiplicação e divisão com sinais — “jogo de sinais”).

Quero estudar com Mapas Mentais

Exemplos resolvidos (passo a passo)

Exemplo 1 — Comparar lados a partir dos ângulos

No triângulo \(ABC\), \( \alpha = 72^\circ \) e \( \beta = 48^\circ \). Compare \(a\) e \(b\).

Ângulo maior ↔ lado oposto maior
\(\alpha = 72^\circ > \beta = 48^\circ\)
\(\Rightarrow a > b\)

Exemplo 2 — Comparar ângulos a partir dos lados

Sabendo que \(a = 13\) e \(b = 11\), qual relação entre \( \alpha \) e \( \beta \)?

Lado maior ↔ ângulo oposto maior
\(a = 13 > b = 11\)
\(\Rightarrow \alpha > \beta\)

Exemplo 3 — Usando a Lei dos Senos (verificação)

Com \(a=8\) e \(b=10\), prove que \( \alpha < \beta \).

\(\dfrac{a}{\sin\alpha} = \dfrac{b}{\sin\beta}\)
\(\Rightarrow \dfrac{8}{\sin\alpha} = \dfrac{10}{\sin\beta}\)
\(\Rightarrow 8\sin\beta = 10\sin\alpha\)
\(\Rightarrow \dfrac{\sin\beta}{\sin\alpha} = \dfrac{10}{8} = 1{,}25\)
\(\Rightarrow \sin\beta > \sin\alpha \Rightarrow \beta > \alpha\)

eBook Gratuito de Fórmulas Matemáticas — Destaque

Tabelas e resumos de geometria (triângulos, ângulos, áreas) + revisão de operações com inteiros para não errar contas.

Baixar grátis agora

Exercícios propostos (com toggle)

Após cada “=”, mantenha as contas uma abaixo da outra para melhor leitura em celulares.

1) Discursiva — Comparando ângulos

No triângulo \(ABC\), \(a=12\) e \(b=9\). Qual ângulo é maior, \( \alpha \) ou \( \beta \)? Justifique.

Ver solução

Lado maior ↔ ângulo oposto maior
\(a=12 > b=9\)
\(\Rightarrow \alpha > \beta\)

2) Múltipla escolha — Qual lado é o maior?

Se \( \alpha = 40^\circ \), \( \beta = 65^\circ \) e \( \gamma = 75^\circ \), o maior lado é:

\(a\)
\(b\)
\(c\)
Não é possível determinar

Mostrar alternativa correta

Maior ângulo \(= 75^\circ \Rightarrow\) maior lado é o oposto \(\Rightarrow\) c é o maior

Resposta: Letra C.

3) Discursiva — Ordem crescente dos ângulos

Os lados de um triângulo medem \(7\), \(9\) e \(12\). Coloque \( \alpha, \beta, \gamma \) em ordem crescente.

Ver solução

Menor lado \(=7 \Rightarrow\) menor ângulo é o oposto
Depois \(9\), depois \(12\)
\(\Rightarrow\) Ângulos crescentes: oposto a \(7\), oposto a \(9\), oposto a \(12\)

4) Múltipla escolha — Ajuste fino com a Lei dos Senos

Num triângulo, \(a=15\), \(b=14\). Qual alternativa é verdadeira?

\(\alpha < \beta\)
\(\alpha = \beta\)
\(\alpha > \beta\)
Não é possível concluir

Mostrar resposta

\(a=15 > b=14 \Rightarrow \alpha > \beta\)

Gabarito: Letra C.

Links internos e produtos do blog

Soma dos Ângulos Internos — base para deduções com triângulos Soma dos Ângulos Externos — giro total de 360° Teorema do Ângulo Externo — \( \theta = \alpha + \beta \) ENEM Matemática — trilhas, listas e simulados 10 eBooks de Matemática — pacote completo Banco de Questões de Matemática — itens editáveis Mapas Mentais de Matemática — revisão visual rápida eBook Gratuito de Fórmulas Matemáticas — baixe agora

Conclusão

A regra “lado maior ⇔ ângulo oposto maior” é imediata e poderosa para comparar medidas sem cálculos longos. Combine-a com a soma dos internos, a soma dos externos e o teorema do ângulo externo para resolver rapidamente questões de provas.

Próximo passo: baixe o eBook gratuito de Fórmulas e acompanhe as novidades no ENEM Matemática.