Seno e Cosseno de um Número Real
Na circunferência trigonométrica, cada número real \(t\in\mathbb{R}\) está associado a um ponto \(P(t)\) — a imagem de \(t\). Esse ponto é a extremidade do arco \(\widehat{AP}\) medido a partir de \(A=(1,0)\) no sentido anti-horário e com comprimento \(t\).
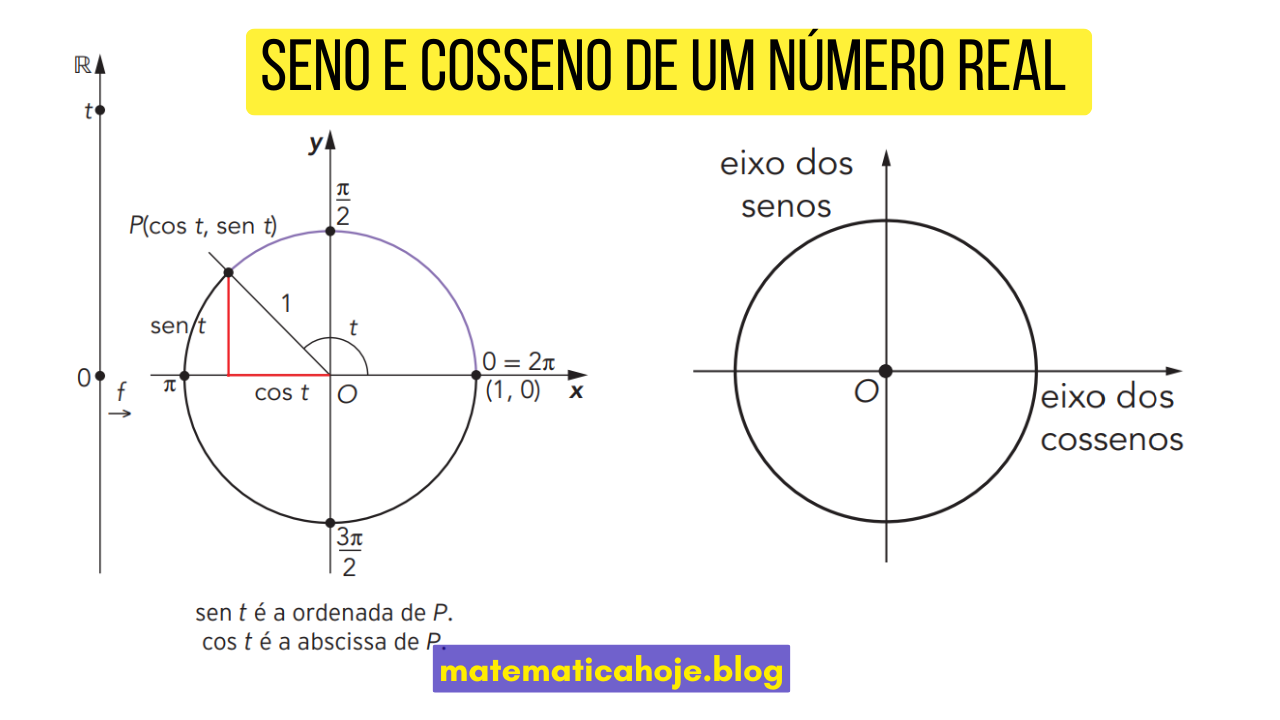
Se \(P(t)=(x,y)\), definimos:
- O cosseno de \(t\) é a abscissa (coordenada \(x\)) do ponto \(P(t)\).
- O seno de \(t\) é a ordenada (coordenada \(y\)) do ponto \(P(t)\).
Observações essenciais
- O eixo das abscissas também é chamado eixo dos cossenos; o eixo das ordenadas é o eixo dos senos.
- Para \(0<t<\pi\), se \(\alpha\) é a abertura do ângulo central que subtende o arco de comprimento \(t\), então \( sen t=sen\alpha \) e \( \cos t=\cos\alpha \). Assim, conectamos seno/cosseno de número real aos de ângulo.
- A relação fundamental vale para todo \(t\in\mathbb{R}\):
\( sen^{2} t + \cos^{2} t = 1 \)
Exemplos rápidos
Exemplo 1. \(t=\dfrac{\pi}{2}\)
O ponto está em \(P=\big(0,1\big)\). Logo \(\cos\left(\frac{\pi}{2}\right)=0\) e \(sen\left(\frac{\pi}{2}\right)=1\).
Exemplo 2. \(t=\pi\)
\(P=(-1,0)\). Assim, \(\cos(\pi)=-1\) e \(sen(\pi)=0\).
Exemplo 3. \(t=2\pi\)
Uma volta completa retorna a \(A=(1,0)\). Então \(\cos(2\pi)=1\) e \(sen(2\pi)=0\).
📘 Exercícios de múltipla escolha
1) O ponto \(P(t)\) é \(\left(\frac{\sqrt2}{2},\frac{\sqrt2}{2}\right)\). Qual valor de \(t\) no intervalo \(0\le t\le 2\pi\)?
- \(\dfrac{\pi}{6}\)
- \(\dfrac{\pi}{4}\)
- \(\dfrac{\pi}{3}\)
- \(\dfrac{3\pi}{4}\)
Ver solução
\(\cos t=sen t=\frac{\sqrt2}{2}\Rightarrow t=\frac{\pi}{4}\).
2) Se \(t\) está no 3º quadrante e \(\cos t=-\dfrac{\sqrt{3}}{2}\), então \(sen t\) é:
- \(\dfrac{1}{2}\)
- \(-\dfrac{1}{2}\)
- \(\dfrac{\sqrt{3}}{2}\)
- \(-\dfrac{\sqrt{3}}{2}\)
Ver solução
No 3º quadrante, seno e cosseno são negativos. Com \(\cos t=-\sqrt3/2\), o par notável é \((\cos,sen)=(-\sqrt3/2,-1/2)\).
3) Qual é o valor de \(sen^2 t+\cos^2 t\) para todo \(t\in\mathbb{R}\)?
- \(0\)
- \(\cos 2t\)
- \(sen 2t\)
- \(1\)
Ver solução
Relação fundamental: \(sen^2 t+\cos^2 t=1\).
4) Se \(P(t)=(x,y)\) e \(t=\dfrac{3\pi}{2}\), então:
- \(x=1,\ y=0\)
- \(x=0,\ y=1\)
- \(x=0,\ y=-1\)
- \(x=-1,\ y=0\)
Ver solução
Em \(3\pi/2\) estamos em \( (0,-1)\).
5) Assinale a alternativa correta:
- \(\cos t\) é a ordenada e \(sen t\) é a abscissa de \(P(t)\).
- \(\cos t\) é a abscissa e \(sen t\) é a ordenada de \(P(t)\).
- Ambos são sempre positivos.
- Ambos são sempre negativos.
Ver solução
Correta: B. Cosseno é a abscissa; seno, a ordenada.
🎒 Produtos recomendados do blog
Seleção de materiais para reforçar circunferência trigonométrica, seno e cosseno.
Coleção 10 eBooks – Trigonometria Essencial
Teoria objetiva, exemplos resolvidos e listas graduadas com gabarito.
Mapas Mentais de Matemática
Esquemas de sinais por quadrante, ângulos notáveis e relações fundamentais.
Banco de Questões – Matemática
Centenas de itens por habilidade: leitura de \(P(t)\), valores notáveis e aplicações.
ENEM Matemática
Roteiro de estudo, resumos e baterias de exercícios focadas no exame.
Canais Oficiais de Matemática
Links verificados para acompanhar novidades, listas e materiais extras.
Para continuar estudando
- Circunferência trigonométrica
- Quadrantes e sinais
- Ângulos notáveis
- Relação fundamental no triângulo retângulo
Este conteúdo conecta geometria e funções trigonométricas, servindo de base para ondas, oscilações e modelos periódicos.





















