Resolver sistemas de equações é um dos tópicos mais cobrados em provas de ensino médio, concursos e no ENEM. Apesar disso, muitos estudantes sentem dificuldade para escolher o método correto ou organizar as contas. Neste artigo completo, você vai aprender a resolver sistemas de equações usando os principais métodos: substituição e adição (ou eliminação). Tudo explicado de forma simples, com exemplos práticos, passo a passo e exercícios com solução detalhada.
Este conteúdo foi desenvolvido com base em anos de experiência em sala de aula e nas questões mais cobradas em vestibulares. Aproveite o artigo, veja os exemplos e baixe também o eBook gratuito com todas as fórmulas de matemática — um material essencial para suas revisões.
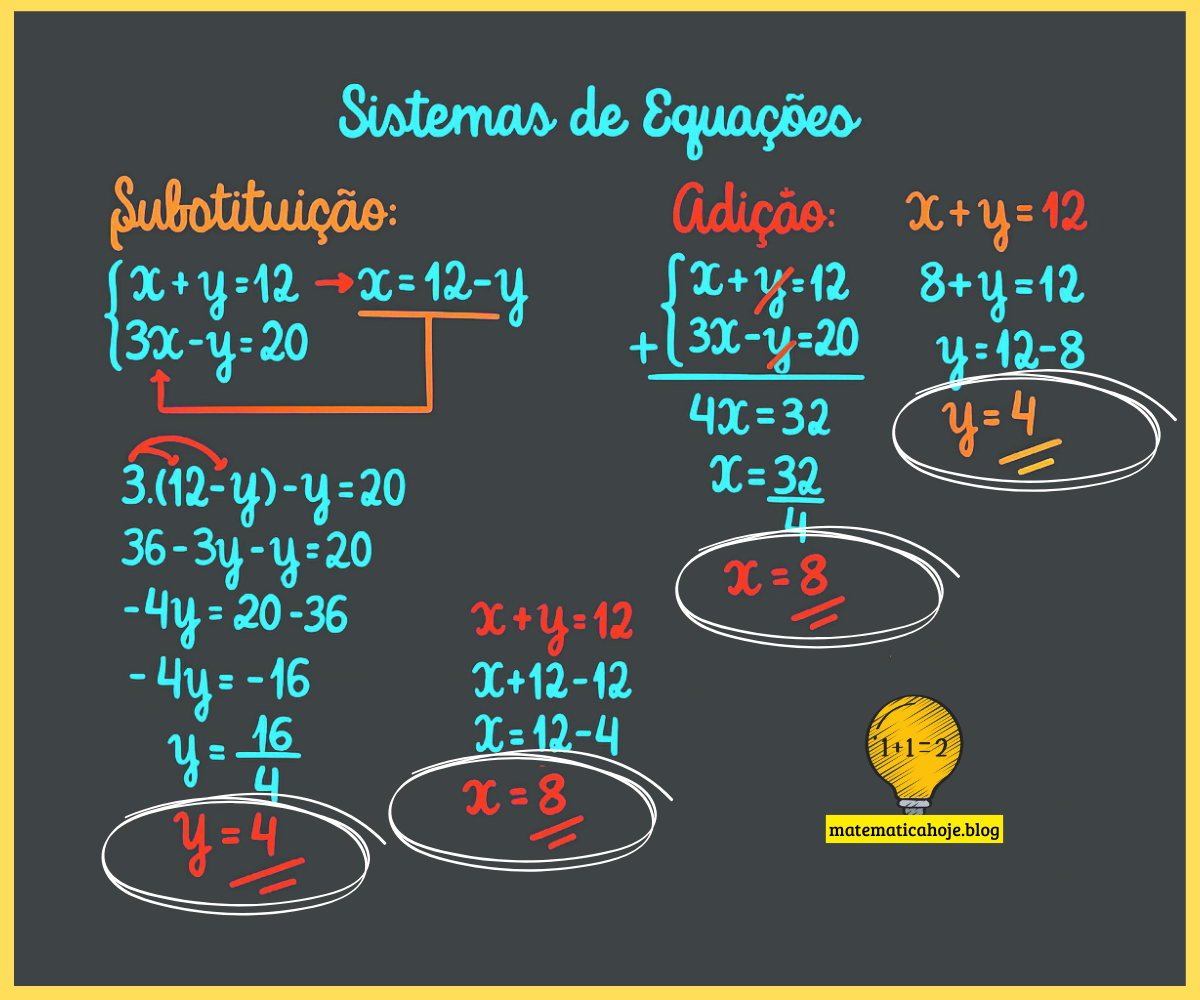
Método da substituição explicado de maneira simples
O método da substituição consiste em isolar uma das incógnitas em uma equação e substituí-la na outra. É um método muito útil quando o sistema possui alguma equação já “quase isolada”.
Exemplo prático usando substituição
Sistema:
\[ \begin{cases} x + y = 12 \\ 3x – y = 20 \end{cases} \]Passo 1: Isolar \(x\) na primeira equação.
\[ x = 12 – y \]Passo 2: Substituir na segunda equação.
\[ 3(12 – y) – y = 20 \] \[ 36 – 3y – y = 20 \] \[ -4y = 20 – 36 \] \[ -4y = -16 \] \[ y = 4 \]Passo 3: Substituir o valor de \(y\) em \(x = 12 – y\)
\[ x = 12 – 4 \] \[ x = 8 \]Método da adição (eliminação) explicado de forma objetiva
O método da adição consiste em somar as equações de forma que uma das incógnitas seja eliminada. É extremamente eficiente quando os coeficientes já estão opostos.
Exemplo prático pelo método da adição
\[ \begin{cases} x + y = 12 \\ 3x – y = 20 \end{cases} \]Somando as duas equações:
\[ 4x = 32 \] \[ x = 8 \]Substituindo em \(x + y = 12\):
\[ 8 + y = 12 \] \[ y = 4 \]Lista de Exercícios Resolvidos de Sistemas de Equações
Exercício 1 — Enunciado atrativo
Qual é o valor de \(x\) e \(y\) no sistema abaixo?
\[ \begin{cases} 2x + y = 14 \\ x – y = 1 \end{cases} \]Ver solução passo a passo
\[ x – y = 1 \] \[ x = 1 + y \] Substituindo: \[ 2(1+y) + y = 14 \] \[ 2 + 2y + y = 14 \] \[ 3y = 12 \] \[ y = 4 \] \[ x = 1 + 4 = 5 \] Resposta: \(x = 5\), \(y = 4\).Exercício 2 — Situação cotidiana
Dois números somam 30 e a diferença entre eles é 6. Quais são esses números?
Ver solução passo a passo
\[ x + y = 30 \] \[ x – y = 6 \] Somando: \[ 2x = 36 \] \[ x = 18 \] \[ 18 + y = 30 \] \[ y = 12 \] Resposta: 18 e 12.Conclusão
Sistemas de equações aparecem em praticamente todas as provas, e dominar os métodos de substituição e adição é fundamental para resolver questões com rapidez e confiança. Esperamos que os exemplos, explicações lineares e exercícios resolvidos tenham ajudado você a visualizar melhor cada etapa. Para revisar ainda mais, baixe os materiais gratuitos e continue explorando os conteúdos recomendados ao longo do artigo.
FAQ — Perguntas Frequentes
Qual é o método mais rápido para resolver sistemas de equações?
O método da adição costuma ser o mais rápido quando os coeficientes permitem eliminar uma incógnita rapidamente. Porém, quando uma equação já tem uma variável isolada, o método da substituição é mais eficiente.
Preciso decorar fórmulas para resolver sistemas?
Não é necessário decorar fórmulas, apenas compreender o processo: isolar uma variável na substituição ou eliminar uma variável na adição. Treino e organização são essenciais para agilizar as contas.
Sistemas caem muito no ENEM?
Sim! Sistemas aparecem em questões de modelos, problemas do cotidiano, geometria analítica e funções. Saber resolver rapidamente aumenta muito o desempenho na prova.
Autor: Adriano Rocha










