Sólidos de Platão — definição, propriedades e fórmulas
Os cinco poliedros convexos regulares: tetraedro, cubo, octaedro, dodecaedro e icosaedro. Veja contagens \(V\), \(E\), \(F\), dualidade, fórmulas de área/volume e exercícios resolvidos.
1) O que são os Sólidos de Platão?
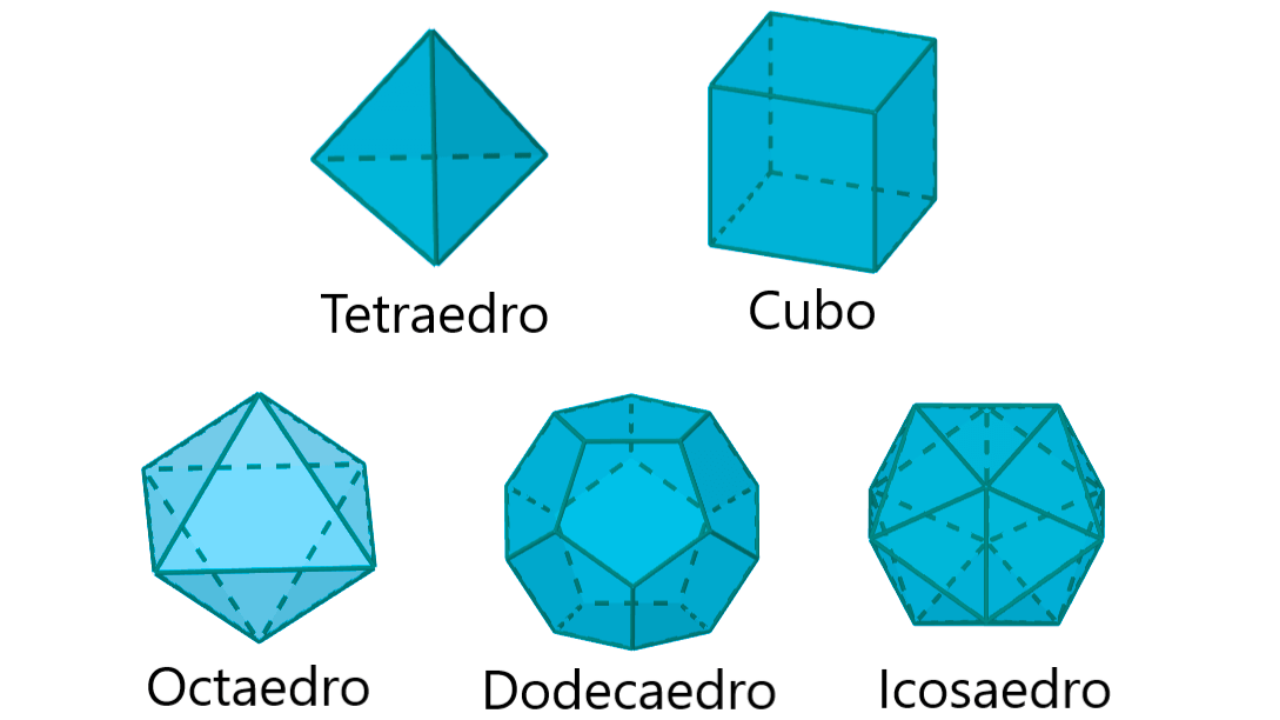
São os únicos poliedros convexos regulares: todas as faces são polígonos regulares congruentes e o mesmo número de faces se encontra em cada vértice. Eles obedecem à Fórmula de Euler (para convexos):
Há exatamente cinco: tetraedro, cubo, octaedro, dodecaedro e icosaedro.
2) Resumo em números (aresta \(a\))
| Sólido | Faces (tipo) | F | V | E | Área total \(A\) | Volume \(V\) |
|---|---|---|---|---|---|---|
| Tetraedro | 4 triângulos equiláteros | 4 | 4 | 6 | \(A=\sqrt{3}\,a^2\) | \(V=\dfrac{a^3}{6\sqrt{2}}\) |
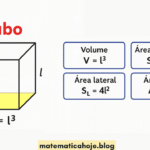
| Cubo | 6 quadrados | 6 | 8 | 12 | \(A=6a^2\) | \(V=a^3\) |
| Octaedro | 8 triângulos equiláteros | 8 | 6 | 12 | \(A=2\sqrt{3}\,a^2\) | \(V=\dfrac{\sqrt{2}}{3}\,a^3\) |
| Dodecaedro | 12 pentágonos regulares | 12 | 20 | 30 | \(A=3\sqrt{25+10\sqrt{5}}\,a^2\) | \(V=\dfrac{15+7\sqrt{5}}{4}\,a^3\) |
| Icosaedro | 20 triângulos equiláteros | 20 | 12 | 30 | \(A=5\sqrt{3}\,a^2\) | \(V=\dfrac{5(3+\sqrt{5})}{12}\,a^3\) |
As fórmulas acima são clássicas e amplamente utilizadas em problemas de olimpíada e vestibulares.
3) Dualidade
Dual de um poliedro: trocamos faces por vértices preservando arestas. Nos Sólidos de Platão:
- Tetraedro ↔ tetraedro (auto-dual);
- Cubo ↔ octaedro;
- Dodecaedro ↔ icosaedro.
4) Exemplos resolvidos (contas na vertical)
-
Enunciado. Um cubo tem aresta \(a=7\ \text{cm}\). Calcule a área total e o volume.
Ver solução
Área total
$$\begin{aligned} A&=6a^2\\ &=6\cdot7^2\\ &=6\cdot49\\ &=\mathbf{294\ \text{cm}^2} \end{aligned}$$Volume
$$\begin{aligned} V&=a^3\\ &=7^3\\ &=7\cdot7\cdot7\\ &=49\cdot7\\ &=\mathbf{343\ \text{cm}^3} \end{aligned}$$ -
Enunciado. Um tetraedro regular tem aresta \(a=12\ \text{cm}\). Calcule o volume.
Ver solução
$$\begin{aligned} V&=\frac{a^3}{6\sqrt{2}}\\ &=\frac{12^3}{6\sqrt{2}}\\ &=\frac{1728}{6\sqrt{2}}\\ &=\frac{288}{\sqrt{2}}\\ &=\frac{288\sqrt{2}}{2}\\ &=\mathbf{144\sqrt{2}\ \text{cm}^3} \end{aligned}$$ -
Enunciado. Um octaedro regular tem aresta \(a=9\ \text{cm}\). Calcule a área total.
Ver solução
$$\begin{aligned} A&=2\sqrt{3}\,a^2\\ &=2\sqrt{3}\cdot9^2\\ &=2\sqrt{3}\cdot81\\ &=\mathbf{162\sqrt{3}\ \text{cm}^2} \end{aligned}$$ -
Enunciado. Um dodecaedro regular tem aresta \(a=4\ \text{cm}\). Calcule o volume (use a expressão da tabela).
Ver solução
$$\begin{aligned} V&=\frac{15+7\sqrt{5}}{4}\,a^3\\ &=\frac{15+7\sqrt{5}}{4}\cdot4^3\\ &=\frac{15+7\sqrt{5}}{4}\cdot64\\ &=16(15+7\sqrt{5})\\ &=\mathbf{240+112\sqrt{5}\ \text{cm}^3} \end{aligned}$$ -
Enunciado. Um icosaedro regular tem aresta \(a=5\ \text{cm}\). Calcule a área total.
Ver solução
$$\begin{aligned} A&=5\sqrt{3}\,a^2\\ &=5\sqrt{3}\cdot25\\ &=\mathbf{125\sqrt{3}\ \text{cm}^2} \end{aligned}$$
5) Curiosidades e aplicações
- Dualidade ajuda a transportar resultados (ex.: do cubo para o octaedro).
- Em química e cristalografia, aparecem como arranjos de coordenação e células unitárias.
- Na computação gráfica, servem de base para malhas simples e subdivisões (como a “esfera icosaédrica”).
6) Exercícios rápidos (com gabarito em abre/fecha)
-
Um icosaedro regular tem área total \(A=500\sqrt{3}\ \text{cm}^2\). Calcule a aresta \(a\).
Gabarito
$$\begin{aligned} 5\sqrt{3}\,a^2&=500\sqrt{3}\\ a^2&=100\\ a&=\mathbf{10\ \text{cm}} \end{aligned}$$ -
Em um tetraedro regular, o volume é \(V=24\sqrt{2}\ \text{cm}^3\). Encontre \(a\).
Gabarito
$$\begin{aligned} \frac{a^3}{6\sqrt{2}}&=24\sqrt{2}\\ a^3&=24\sqrt{2}\cdot6\sqrt{2}=24\cdot6\cdot2=288\\ a&=\sqrt[3]{288}=\mathbf{ \approx 6.62\ \text{cm}} \end{aligned}$$ -
Mostre que os pares (cubo, octaedro) e (dodecaedro, icosaedro) satisfazem Euler com os mesmos \(E\).
Gabarito
Para cubo: \(V=8,\ E=12,\ F=6\Rightarrow 8-12+6=2\).
Para octaedro: \(V=6,\ E=12,\ F=8\Rightarrow 6-12+8=2\).
Para dodecaedro: \(20-30+12=2\); para icosaedro: \(12-30+20=2\). Em cada par dual, \(E\) coincide.